题目内容
直线l：y=mx+n（m、n是常数）的图象如图所示，
化简：
．
解：∵函数图象过一、三、四象限，
∴m＞0，n＜0，
∴原式=m-n-（-n）-（m+1）
=m-n+n-m-1
=-1．
分析：根据函数图象过一、三、四象限可判断m＞0，n＜0，据此，根据绝对值的性质去绝对值、开方，然后进行加减运算．
点评：本题考查了一次函数图象与系数的关系，同时要熟悉绝对值的性质和二次根式的性质．
∴m＞0，n＜0，
∴原式=m-n-（-n）-（m+1）
=m-n+n-m-1
=-1．
分析：根据函数图象过一、三、四象限可判断m＞0，n＜0，据此，根据绝对值的性质去绝对值、开方，然后进行加减运算．
点评：本题考查了一次函数图象与系数的关系，同时要熟悉绝对值的性质和二次根式的性质．
练习册系列答案
阅读快车系列答案
相关题目
在平面直角坐标系xOy中，已知关于x的二次函数y=x2+（k-1）x+2k-1的图象与x轴交于A、B两点（点A在点B左侧），与y轴交于点C，其中k是一元二次方程p2-p-2=0的根，且k＜0．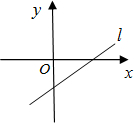
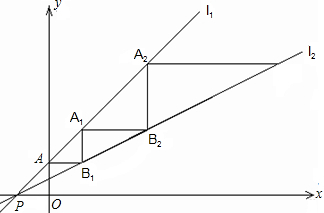
（2012•花都区一模）直线l：y=mx+n（m、n是常数）的图象如图所示，
（2013•盐城模拟）如图，直线l1：y1=x+1与直线l2：y2=mx+n相交于点P（1，b）．当y1＞y2时，x的取值范围为
如图，直线y=kx+2与x轴、y轴分别交于点A、B，点C（1，a）是该直线与双曲线y=