题目内容
9.下列函数中,在0≤x≤2上y随x的增大而增大的是( )| A. | y=-x+1 | B. | y=x2-4x+5 | C. | y=x2 | D. | y=$\frac{2}{x}$ |
分析 根据函数的增减性判断各个选项,选出在定义域内y随x的增大而增大的函数即可.
解答 解:A、y=-x+1在0≤x≤2上y随x的增大而减小,此选项错误;
B、y=x2-4x+5在0≤x≤2上y随x的增大而减小,此选项错误;
C、y=x2在0≤x≤2上y随x的增大而增大,此选项正确;
D、y=$\frac{2}{x}$在0≤x≤2上y随x的增大而减小,此选项错误;
故选C.
点评 本题考查了二次函数的性质、一次函数的性质以及反比例函数的性质,解答本题的关键是掌握各个函数在其定义域内的增减性,同学们要特别注意反比例函数的增减性问题,要在每个象限内进行讨论.

练习册系列答案
相关题目
17.已知命题“关于x的一元二次方程x2+bx+1=0,当b<0时必有实数解”,能说明这个命题是假命题的一个反例是( )
| A. | b=0 | B. | b=-1 | C. | b=2 | D. | b=-2 |
14.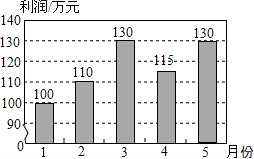 某企业1~5月份的利润情况如图所示,则下列说法中正确的是( )
某企业1~5月份的利润情况如图所示,则下列说法中正确的是( )
 某企业1~5月份的利润情况如图所示,则下列说法中正确的是( )
某企业1~5月份的利润情况如图所示,则下列说法中正确的是( )| A. | 1~2月份利润的增长快于2~3月份利润的增长 | |
| B. | 1~4月份利润的极差于1~5月份利润的极差不同 | |
| C. | 1~5月份利润的中位数是120万元 | |
| D. | 1~5月份利润的众数是130万元 |
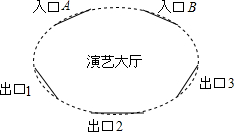 某演艺大厅有2个入口和3个出口,其示意图如下,参观者从任意一个入口进入,参观结束后从任意一个出口离开
某演艺大厅有2个入口和3个出口,其示意图如下,参观者从任意一个入口进入,参观结束后从任意一个出口离开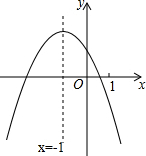 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论: