题目内容
若对0<x<3上的一切实数x,不等式(m-2)x<2m-1恒成立,则实数m的取值范围是
- A.

- B.

- C.

- D.

B
分析:先变形(m-2)x<2m-1得到(x-2)m<2x-1,讨论:当0<x<2,m>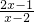 ,即m>2+
,即m>2+ ;当x=2时,(x-2)m<2x-1恒成立;当2<x<3时,m<
;当x=2时,(x-2)m<2x-1恒成立;当2<x<3时,m<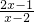 ,即m<2+
,即m<2+ ,而对0<x<3上的一切实数x,不等式(m-2)x<2m-1恒成立,当x=0,m取最小值
,而对0<x<3上的一切实数x,不等式(m-2)x<2m-1恒成立,当x=0,m取最小值 ,x=3时,m取最大值5,然后综合得到m的范围.
,x=3时,m取最大值5,然后综合得到m的范围.
解答:(m-2)x<2m-1变形得(x-2)m<2x-1,
当0<x<2,m>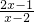 ,即m>2+
,即m>2+ ,
,
∵对0<x<3上的一切实数x,不等式(m-2)x<2m-1恒成立,
∴x=0,m取最小值,m≥2- ,即m≥
,即m≥ ;
;
当x=2时,(x-2)m<2x-1恒成立,
当2<x<3时,m<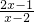 ,即m<2+
,即m<2+ ,
,
∴x=3时,m取最大值,m≤2+3,即m≤5,
∴实数m的取值范围是 ≤m≤5.
≤m≤5.
故选B.
点评:本题考查了解一元一次不等式:根据不等式的性质先去括号(或去分母),再把含未知数的项移到不等式的左边,常数项移到右边,合并同类项后,然后把未知数的系数化为1即可.
分析:先变形(m-2)x<2m-1得到(x-2)m<2x-1,讨论:当0<x<2,m>
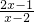 ,即m>2+
,即m>2+ ;当x=2时,(x-2)m<2x-1恒成立;当2<x<3时,m<
;当x=2时,(x-2)m<2x-1恒成立;当2<x<3时,m<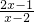 ,即m<2+
,即m<2+ ,而对0<x<3上的一切实数x,不等式(m-2)x<2m-1恒成立,当x=0,m取最小值
,而对0<x<3上的一切实数x,不等式(m-2)x<2m-1恒成立,当x=0,m取最小值 ,x=3时,m取最大值5,然后综合得到m的范围.
,x=3时,m取最大值5,然后综合得到m的范围.解答:(m-2)x<2m-1变形得(x-2)m<2x-1,
当0<x<2,m>
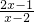 ,即m>2+
,即m>2+ ,
,∵对0<x<3上的一切实数x,不等式(m-2)x<2m-1恒成立,
∴x=0,m取最小值,m≥2-
 ,即m≥
,即m≥ ;
;当x=2时,(x-2)m<2x-1恒成立,
当2<x<3时,m<
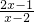 ,即m<2+
,即m<2+ ,
,∴x=3时,m取最大值,m≤2+3,即m≤5,
∴实数m的取值范围是
 ≤m≤5.
≤m≤5.故选B.
点评:本题考查了解一元一次不等式:根据不等式的性质先去括号(或去分母),再把含未知数的项移到不等式的左边,常数项移到右边,合并同类项后,然后把未知数的系数化为1即可.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
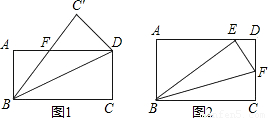
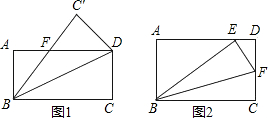 矩形折叠问题:如图所示,把一张矩形纸片沿对角线折叠,重合部分是什么图形,试说明理由.
矩形折叠问题:如图所示,把一张矩形纸片沿对角线折叠,重合部分是什么图形,试说明理由.
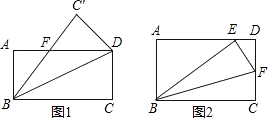 矩形折叠问题:如图所示,把一张矩形纸片沿对角线折叠,重合部分是什么图形,试说明理由.
矩形折叠问题:如图所示,把一张矩形纸片沿对角线折叠,重合部分是什么图形,试说明理由.