题目内容
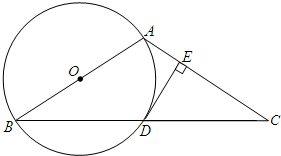 如图,以△ABC的边AB为直径的⊙O经过BC的中点D,过D作DE⊥AC于E.
如图,以△ABC的边AB为直径的⊙O经过BC的中点D,过D作DE⊥AC于E.(1)求证:AB=AC;
(2)求证:DE是⊙O的切线;
(3)若⊙O的半径为3,切线长DE=2
| 2 |
分析:(1)连接AD,AB是直径可得∠ADB=∠ADC=90°,而D是中点则有BD=CD,结合AD=AD,易证△ABD≌△ACD,从而有AB=AC;
(2)连接OD,由O、D是中点易证OD是△ABC的中位线,那么OD∥AC,于是∠ODE=∠CED=90°,即DE是⊙O的切线;
(3)由于∠4+∠3=90°,∠C+∠3=90°,易得∠4=∠C,而∠1=∠2,易证△AED∽△DEC,从而有
=
,由于OA=3,那么AB=AC=6,于是可设AE=x,则CE=6-x,代入比例关系式,易求得x1=2,x2=4,从而可分两种情况来讨论:①当AE=x1=2时,CE=6-2=4,利用勾股定理可先求CD,从而易求cos∠C;②当AE=x2=4时,CE=6-4=2,解法同①.
(2)连接OD,由O、D是中点易证OD是△ABC的中位线,那么OD∥AC,于是∠ODE=∠CED=90°,即DE是⊙O的切线;
(3)由于∠4+∠3=90°,∠C+∠3=90°,易得∠4=∠C,而∠1=∠2,易证△AED∽△DEC,从而有
| AE |
| DE |
| DE |
| CE |
解答: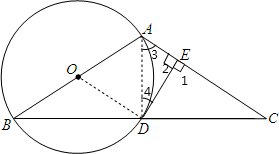 (1)证明:连接AD,
(1)证明:连接AD,
∵AB是⊙O的直径,
∴∠ADB=∠ADC=90°①,
又∵D是BC的中点,
∴BD=CD②,
而AD=AD③,
由①②③得△ABD≌△ACD(SAS),
∴AB=AC;
(2)证明:连接OD,
∵O是AB的中点,D是BC的中点,
∴OD是△ABC的中位线,
∴OD∥AC,
∴∠ODE=∠CED=90°,
即DE⊥OD,
∴DE是⊙O的切线;
(3)解:在Rt△AED中,∠4+∠3=90°,
在Rt△ADC中,∠C+∠3=90°,
∴∠4=∠C,
又∵∠2=∠1,
∴△AED∽△DEC,
∴
=
④,
∵⊙O的半径为3,
∴AB=AC=6,
设AE=x,则CE=6-x,
又DE=2
,
代入④得
=
,
解得x1=2,x2=4,
①当AE=x1=2时,CE=6-2=4,
在Rt△DEC中,CD=
=
=2
,
∴cos∠C=
=
=
,
②当AE=x2=4时,CE=6-4=2,CD=
=
=2
,
∴cos∠C=
=
=
.
 (1)证明:连接AD,
(1)证明:连接AD,∵AB是⊙O的直径,
∴∠ADB=∠ADC=90°①,
又∵D是BC的中点,
∴BD=CD②,
而AD=AD③,
由①②③得△ABD≌△ACD(SAS),
∴AB=AC;
(2)证明:连接OD,
∵O是AB的中点,D是BC的中点,
∴OD是△ABC的中位线,
∴OD∥AC,
∴∠ODE=∠CED=90°,
即DE⊥OD,
∴DE是⊙O的切线;
(3)解:在Rt△AED中,∠4+∠3=90°,
在Rt△ADC中,∠C+∠3=90°,
∴∠4=∠C,
又∵∠2=∠1,
∴△AED∽△DEC,
∴
| AE |
| DE |
| DE |
| CE |
∵⊙O的半径为3,
∴AB=AC=6,
设AE=x,则CE=6-x,
又DE=2
| 2 |
代入④得
| x | ||
2
|
2
| ||
| 6-x |
解得x1=2,x2=4,
①当AE=x1=2时,CE=6-2=4,
在Rt△DEC中,CD=
| DE2+CE2 |
(2
|
| 6 |
∴cos∠C=
| CE |
| CD |
| 4 | ||
2
|
| ||
| 3 |
②当AE=x2=4时,CE=6-4=2,CD=
| DE2+CE2 |
(2
|
| 3 |
∴cos∠C=
| CE |
| CD |
| 2 | ||
2
|
| ||
| 3 |
点评:本题考查了全等三角形的判定和性质、三角形中位线定理、切线的判定、相似三角形的判定和性质、勾股定理、三角函数的计算.解题的关键是连接OD、AD,构造直角三角形和平行线.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 26、如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形.
26、如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形. 如图,以△ABC的边AB为直径作⊙O,交BC于D点,交AC于E点,BD=DE
如图,以△ABC的边AB为直径作⊙O,交BC于D点,交AC于E点,BD=DE
 (2011•峨眉山市二模)如图,以△ABC的边AB为直径作⊙O,BC与⊙O交于D,D是BC的中点,过D作DE⊥AC,交AC于点E.
(2011•峨眉山市二模)如图,以△ABC的边AB为直径作⊙O,BC与⊙O交于D,D是BC的中点,过D作DE⊥AC,交AC于点E. (2010•黔东南州)如图,以△ABC的边BC为直径作⊙O分别交AB,AC于点F.点E,AD⊥BC于D,AD交于⊙O于M,交BE于H.
(2010•黔东南州)如图,以△ABC的边BC为直径作⊙O分别交AB,AC于点F.点E,AD⊥BC于D,AD交于⊙O于M,交BE于H. 如图,以△ABC的边AB为直径的⊙O交AC于点D,弦DE∥AB,∠C=∠BAF
如图,以△ABC的边AB为直径的⊙O交AC于点D,弦DE∥AB,∠C=∠BAF