Question

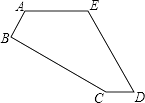
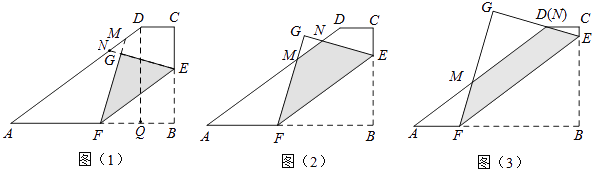
【题目】如图，在梯形ABCD中，AB∥DC，∠B=90°，且AB=10，BC=6，CD=2．点E从点B出发沿BC方向运动，过点E作EF∥AD交边AB于点F．将△BEF沿EF所在的直线折叠得到△GEF，直线FG、EG分别交AD于点M、N，当EG过点D时，点E即停止运动．设BE=x，△GEF与梯形ABCD的重叠部分的面积为y．

（1）证明△AMF是等腰三角形；
（2）当EG过点D时（如图（3）），求x的值；
（3）将y表示成x的函数，并求y的最大值．

Answer 1

【答案】
（1）

证明：如图1，∵EF∥AD，

∴∠A=∠EFB，∠GFE=∠AMF．

∵△GFE与△BFE关于EF对称，

∴△GFE≌△BFE，

∴∠GFE=∠BFE，

∴∠A=∠AMF，

∴△AMF是等腰三角形

（2）

解：如图1，作DQ⊥AB于点Q，

∴∠AQD=∠DQB=90°．

∵AB∥DC，

∴∠CDQ=90°．

∵∠B=90°，

∴四边形CDQB是矩形，

∴CD=QB=2，QD=CB=6，

∴AQ=10﹣2=8．

在Rt△ADQ中，由勾股定理得

AD= =10，

∴tan∠A= ，

∴tan∠EFB= =

如图3，∵EB=x，

∴FB= x，CE=6﹣x，

∴AF=MF=10﹣ x，

∴GM= ，

∴GD=2x﹣ ，

∴DE= ﹣x，

在Rt△CED中，由勾股定理得

（ ﹣x）2﹣（6﹣x）2=4，

解得：x= ，

∴当EG过点D时x= ；

（3）

解：当点G在梯形ABCD内部或边AD上时，

y= x x= x2，

当点G在边AD上时，GM= =0，求得x= ，

此时0＜x≤ ，

则当x= 时，y最大值为 ．

当点G在梯形ABCD外时，

∵△GMN∽△GFE，

∴ ，

即 ，由（2）知，x≤ ，

y=﹣2x2+20x﹣ =﹣2（x﹣5）2+ （ ＜x≤ ），

当x=5时，y最大值为 ，

由于 ＞ ，故当x=5时，y最大值为

【解析】（1）由条件EF∥AD就可以得出∠A=∠EFB，∠GFE=∠AMF，由△GFE与△BFE关于EF对称可以得出∠GFE=∠BFE，就可以得出∠A=∠AMF，从而得出结论；（2）当EG过点D时在Rt△EDC中由勾股定理建立方程求出其解即可；（3）分情况讨论当点G不在梯形外时和点G在梯形之外两种情况求出x的值就可以求出y与x之间的函数关系式，在自变量的取值范围内就可以求出相应的最大值，从而求出结论；
【考点精析】掌握等腰三角形的性质和勾股定理的概念是解答本题的根本，需要知道等腰三角形的两个底角相等（简称：等边对等角）；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．