题目内容
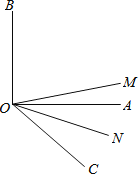
【题目】如图,∠AOB=90°,OC,OD分别是∠AOE,∠BOE的平分线.
(1)求∠COD的度数;
(2)若∠AOB=α°,其他条件不变,则∠COD= °;
(3)你从(1),(2)的结果中能发现什么规律?(不必证明)
【答案】(1)∠COD=45°;(2)![]() α;(3)∠COD的大小总等于∠AOB的一半.
α;(3)∠COD的大小总等于∠AOB的一半.
【解析】
(1)(1)根据题意,易得∠EOC= ![]() ∠AOC,∠DOE=
∠AOC,∠DOE= ![]() ∠BOE进而结合∠COD=∠EOC -∠DOE的关系,易得答案;
∠BOE进而结合∠COD=∠EOC -∠DOE的关系,易得答案;
(2)由(1)的结论,易得当∠AOB=α时,总有∠DOE = ![]() ∠AOB的关系,即的答案;
∠AOB的关系,即的答案;
(3)分析(1)(2)的结论,易得答案.
(1)∵OC,OD分别是∠AOE,∠BOE的平分线.
∴∠EOC= ![]() ∠AOC,∠DOE=
∠AOC,∠DOE= ![]() ∠BOE
∠BOE
∴∠COD=∠COE-∠DOE=![]() ∠AOE-
∠AOE-![]() ∠BOE=
∠BOE=![]() (∠AOE-∠BOE)=
(∠AOE-∠BOE)=![]() ∠AOB=
∠AOB=![]() ×90°=45°;
×90°=45°;
(2)![]() α;
α;
(3)∠COD的大小总等于∠AOB的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目