题目内容
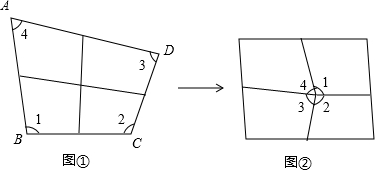
 如图1是四边形纸片ABCD,其中∠B=120°,∠D=50°.如果将其右下角向内折出△PCR,如图2所示,恰使CP∥AB,RC∥AD,则∠C的度数为
如图1是四边形纸片ABCD,其中∠B=120°,∠D=50°.如果将其右下角向内折出△PCR,如图2所示,恰使CP∥AB,RC∥AD,则∠C的度数为
- A.105°
- B.100°
- C.95°
- D.90°
C
分析:根据平行线的性质得∠BPC=180°-∠B=60°,∠DRC=130°,再利用三角形的内角和求出∠C的度数.
解答:∵CP∥AB,RC∥AD
∴∠BPC=180°-∠B=60°,∠DRC=130°
∴∠C=180°-60°-25°=95°.
故选C.
点评:主要考查了三角形的内角和外角之间的关系平行线的性质和翻折变换.(1)三角形的外角等于与它不相邻的两个内角和.(2)三角形的内角和是180度.求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件.
分析:根据平行线的性质得∠BPC=180°-∠B=60°,∠DRC=130°,再利用三角形的内角和求出∠C的度数.
解答:∵CP∥AB,RC∥AD
∴∠BPC=180°-∠B=60°,∠DRC=130°
∴∠C=180°-60°-25°=95°.
故选C.
点评:主要考查了三角形的内角和外角之间的关系平行线的性质和翻折变换.(1)三角形的外角等于与它不相邻的两个内角和.(2)三角形的内角和是180度.求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 7、如图1是四边形纸片ABCD,其中∠B=120°,∠D=50°.如果将其右下角向内折出△PCR,如图2所示,恰使CP∥AB,RC∥AD,则∠C的度数为( )
7、如图1是四边形纸片ABCD,其中∠B=120°,∠D=50°.如果将其右下角向内折出△PCR,如图2所示,恰使CP∥AB,RC∥AD,则∠C的度数为( )