题目内容
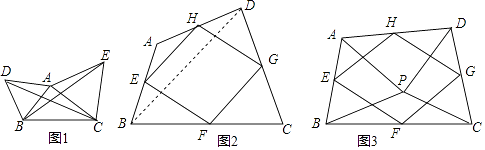
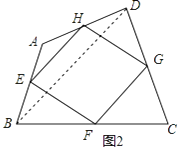
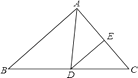
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径作圆
为直径作圆![]() ,分别交
,分别交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 交线段
交线段![]() 于点
于点![]() .
.
(1)求证:![]() 是圆
是圆![]() 的切线;
的切线;
(2)若![]() 为
为![]() 的中点,求
的中点,求![]() 的值;
的值;
(3)若![]() ,求圆
,求圆![]() 的半径.
的半径.
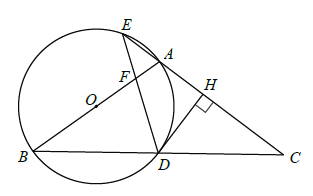
【答案】(1)证明见解析(2)![]() ,(3)
,(3)![]()
【解析】
试题分析:(1)连接OD,然后可得等腰三角形,然后通过等腰三角形的性质求得OD∥AC,然后可根据切线的判定求证即可;
(2)根据等腰三角形的性质和三角形的中位线可证得△AEF∽△ODF,由相似三角形的性质可求解;
(3)根据等腰三角形的性质,和圆的有关性质,可证明△BFD∽△EFA,然后根据相似三角形的性质可求解.
试题解析:(1)
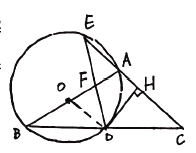
连接![]() ,
,
∵![]() ,
,
∴![]() 是等腰三角形,
是等腰三角形,
![]() ①,
①,
又在![]() 中, ∵
中, ∵![]() ,
,
∴![]() ②,
②,
则由①②得,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 是
是![]() 的切线;
的切线;
(2)
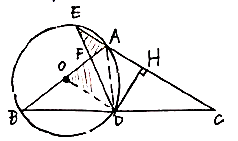
在![]() 中, ∵
中, ∵![]() ,
,
∵由![]() 中可知,
中可知,![]() ,
,
![]() 是等腰三角形,
是等腰三角形,
又∵![]() 且点
且点![]() 是
是![]() 中点,
中点,
∴设![]() ,则
,则![]() ,
,
连接![]() ,则在
,则在![]() 中,
中,![]() ,即
,即![]() ,
,
又∵![]() 是等腰三角形,∴
是等腰三角形,∴![]() 是
是![]() 中点,
中点,
则在![]() 中,
中,![]() 是中位线, ∴
是中位线, ∴![]() ,
,
∵![]() , ∴
, ∴![]() ,
,
在![]() 和
和![]() 中,
中,![]() , ∴
, ∴![]() ,
,
∴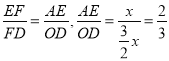 ,
,
∴![]() .
.
(3)设![]() 半径为
半径为![]() ,即
,即![]() ,
,
∵![]() , ∴
, ∴![]() ,
,
又∵![]() , ∴
, ∴![]() ,
,
则![]() , ∴
, ∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中, ∵
中, ∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() 是等腰三角形,
是等腰三角形,
∴![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中
中![]() ,∵
,∵![]() ,
,
∴![]() ,
,
解得![]() (舍)
(舍)
∴综上,![]() 的半径为
的半径为![]() .
.

练习册系列答案
相关题目