题目内容
如图,函数 (x>0,k>0)的图象经过A(1,4),B(m,n),其中m>1,过点A作x轴的
(x>0,k>0)的图象经过A(1,4),B(m,n),其中m>1,过点A作x轴的 垂线,垂足为C,过点B作y轴的垂线,垂足为D,连接AD,DC,CB,AC与BD相交于点E.
垂线,垂足为C,过点B作y轴的垂线,垂足为D,连接AD,DC,CB,AC与BD相交于点E.(1)若△ABD的面积为4,求点B的坐标;
(2)若四边形ABCD是等腰梯形,求出直线AB的函数解析式.
【答案】分析:(1)根据k=1×4=mn,求k及mn的值,再由S△ABD=4,即 m•(4-n)=4,求m及n的值,确定B点坐标;
m•(4-n)=4,求m及n的值,确定B点坐标;
(2)由ABCD为等腰梯形可知AC=BD,且A(1,4)可知B(4,1),设直线AB的解析式为y=kx+b,利用待定系数法求直线AB的解析式.
解答: 解:(1)由题意,得k=1×4=4,mn=4,
解:(1)由题意,得k=1×4=4,mn=4,
∵S△ABD=4,∴ m•(4-n)=4,
m•(4-n)=4,
2m- mn=4,∴2m=6,m=3,
mn=4,∴2m=6,m=3,
∴n= ,∴B(3,
,∴B(3, );
);
(2)∵等腰梯形ABCD中,AC=BD,∴B(4,1),
设直线AB的解析式为y=kx+b,
则 解得
解得
∴直线AB的解析式为y=-x+5.
点评:本题考查反比例函数性质的综合运用.注意反比例函数的系数与得的坐标的关系,三角形面积与点的坐标的关系,通过解方程组求直线解析式.同时要注意运用数形结合的思想.
 m•(4-n)=4,求m及n的值,确定B点坐标;
m•(4-n)=4,求m及n的值,确定B点坐标;(2)由ABCD为等腰梯形可知AC=BD,且A(1,4)可知B(4,1),设直线AB的解析式为y=kx+b,利用待定系数法求直线AB的解析式.
解答:
 解:(1)由题意,得k=1×4=4,mn=4,
解:(1)由题意,得k=1×4=4,mn=4,∵S△ABD=4,∴
 m•(4-n)=4,
m•(4-n)=4,2m-
 mn=4,∴2m=6,m=3,
mn=4,∴2m=6,m=3,∴n=
 ,∴B(3,
,∴B(3, );
);(2)∵等腰梯形ABCD中,AC=BD,∴B(4,1),
设直线AB的解析式为y=kx+b,
则
 解得
解得
∴直线AB的解析式为y=-x+5.
点评:本题考查反比例函数性质的综合运用.注意反比例函数的系数与得的坐标的关系,三角形面积与点的坐标的关系,通过解方程组求直线解析式.同时要注意运用数形结合的思想.

练习册系列答案
相关题目
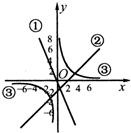 如图,函数图象①、②、③的表达式应为( )
如图,函数图象①、②、③的表达式应为( )A、y=-
| ||||
B、y=
| ||||
C、y=-
| ||||
D、y=-
|
 如图:函数y=-kx(k≠0)与y=-
如图:函数y=-kx(k≠0)与y=-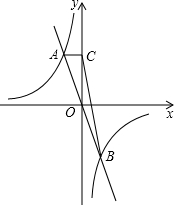 如图,函数y=-kx与
如图,函数y=-kx与 如图,函数y1=k1x+b的图象与函数y2=
如图,函数y1=k1x+b的图象与函数y2=