题目内容
如图，⊙A与x轴相切于点O，点A的坐标为（0，1），点P在⊙A上，且在第一象限，∠PAO=60°，⊙A沿x轴正方向滚动，当点P第n次落在x轴上时，点P的横坐标为________．
π分析：首先根据弧长公式求得弧OP的长，则点P第1次落在x轴上时，点P的横坐标即为弧OP的长；点P第2次落在x轴上时，点P的横坐标即为圆周长加上弧OP的长，以此推广即可求解．
解答：根据弧长公式，得
弧OP的长=
=
，圆周长是2π，则点P第1次落在x轴上时，点P的横坐标是
，点P第2次落在x轴上时，点P的横坐标是2π+=
，以此类推，点P第n次落在x轴上时，点P的横坐标是2（n-1）π+
=π．故答案为：
π．点评：此题考查了弧长公式以及规律的推广．
练习册系列答案
活力课时同步练习册系列答案
学业测评一课一测系列答案
相关题目
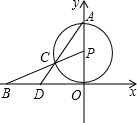轴上．连接BP交⊙P于点C，连接AC并延长交x轴于点D．
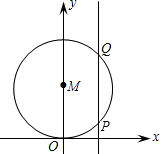如图，⊙M与x轴相切于原点，平行于y轴的直线交圆于P、Q两点，P点在Q点的下方．若P点的坐标是（2，1），求圆心M的坐标．
如图，⊙M与x轴相切于原点，平行于y轴的直线交⊙M于P、Q两点，P点在Q点的下方．若点P的坐标是（2，1），则圆心M的坐标是
（2013•仓山区模拟）如图，⊙M与x轴相切与原点，平行于y轴的直线交⊙M于P、Q两点，P点在Q点的下方，若点P的坐标是
（2012•黔西南州模拟）如图，⊙P与x轴相切于坐标原点O，点A（0，2）是⊙P与y轴的交点，点B（