题目内容
已知函数y1=px+q和y2=ax2+bx+c的图象交于A(1,-1)和B(3,1)两点,抛物线y2与x轴交点的横坐标为x1,x2,且|x1-x2|=2 .
.
(1)求这两个函数的解析式;
(2)设y2与y轴交点为C,求△ABC的面积.
解:(1)将A、B两点坐标代入函数y1=px+q中,得 ,解得
,解得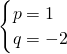 ,
,
∴函数y1=x-2,
由根与系数关系,得x1+x2=- ,x1•x2=
,x1•x2= ,
,
∵|x1-x2|=2 ,∴(x1-x2)2=8,即(x1+x2)2-4x1•x2=8,b2-4ac=8a2,
,∴(x1-x2)2=8,即(x1+x2)2-4x1•x2=8,b2-4ac=8a2,
将A、B两点坐标代入函数y2=ax2+bx+c中,得 ,解得
,解得 或
或 ,
,
∴函数y2= x2-x-
x2-x- 或y2=-
或y2=- x2+3x-
x2+3x- ;
;
(2)当y2= x2-x-
x2-x- 时,C(0,-
时,C(0,- ),
),
S△ABC= ×(1+3)×2-
×(1+3)×2- ×3×(1+
×3×(1+ )-
)- ×1×
×1× =
= ;
;
当y2=- x2+3x-
x2+3x- 时,C(0,-
时,C(0,- ),
),
S△ABC= ×(1+
×(1+ )×3-
)×3- ×(1+3)×2-
×(1+3)×2- ×1×(
×1×( -1)=
-1)= .
.
分析:(1)将A、B两点代入函数y1=px+q中,可求函数解析式,将A、B代入y2=ax2+bx+c中,再利用根与系数关系,列方程组求y2的函数关系式;
(2)根据A、B、C三点坐标,利用组合图形求三角形的面积.
点评:本题考查了二次函数的综合运用.关键是根据条件列方程组求函数解析式,利用组合图形求三角形的面积.
 ,解得
,解得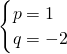 ,
,∴函数y1=x-2,
由根与系数关系,得x1+x2=-
 ,x1•x2=
,x1•x2= ,
,∵|x1-x2|=2
 ,∴(x1-x2)2=8,即(x1+x2)2-4x1•x2=8,b2-4ac=8a2,
,∴(x1-x2)2=8,即(x1+x2)2-4x1•x2=8,b2-4ac=8a2,将A、B两点坐标代入函数y2=ax2+bx+c中,得
 ,解得
,解得 或
或 ,
,∴函数y2=
 x2-x-
x2-x- 或y2=-
或y2=- x2+3x-
x2+3x- ;
;(2)当y2=
 x2-x-
x2-x- 时,C(0,-
时,C(0,- ),
),S△ABC=
 ×(1+3)×2-
×(1+3)×2- ×3×(1+
×3×(1+ )-
)- ×1×
×1× =
= ;
;当y2=-
 x2+3x-
x2+3x- 时,C(0,-
时,C(0,- ),
),S△ABC=
 ×(1+
×(1+ )×3-
)×3- ×(1+3)×2-
×(1+3)×2- ×1×(
×1×( -1)=
-1)= .
.分析:(1)将A、B两点代入函数y1=px+q中,可求函数解析式,将A、B代入y2=ax2+bx+c中,再利用根与系数关系,列方程组求y2的函数关系式;
(2)根据A、B、C三点坐标,利用组合图形求三角形的面积.
点评:本题考查了二次函数的综合运用.关键是根据条件列方程组求函数解析式,利用组合图形求三角形的面积.

练习册系列答案
相关题目
 .
.