题目内容
如图,在矩形 中,
中, ,
, ,点
,点 是边
是边 上的动点(点
上的动点(点 不与点
不与点 ,点
,点 重合),过点
重合),过点 作直线
作直线 ,交
,交 边于
边于 点,再把
点,再把 沿着动直线
沿着动直线 对折,点
对折,点 的对应点是
的对应点是 点,设
点,设 的长度为
的长度为 ,
, 与矩形
与矩形 重叠部分的面积为
重叠部分的面积为 .
.
(1)求 的度数;
的度数;
(2)当 取何值时,点
取何值时,点 落在矩形
落在矩形 的
的 边上?
边上?
(3)①求 与
与 之间的函数关系式;
之间的函数关系式;
②当 取何值时,重叠部分的面积等于矩形面积的
取何值时,重叠部分的面积等于矩形面积的 ?
?
 中,
中, ,
, ,点
,点 是边
是边 上的动点(点
上的动点(点 不与点
不与点 ,点
,点 重合),过点
重合),过点 作直线
作直线 ,交
,交 边于
边于 点,再把
点,再把 沿着动直线
沿着动直线 对折,点
对折,点 的对应点是
的对应点是 点,设
点,设 的长度为
的长度为 ,
, 与矩形
与矩形 重叠部分的面积为
重叠部分的面积为 .
.(1)求
 的度数;
的度数;(2)当
 取何值时,点
取何值时,点 落在矩形
落在矩形 的
的 边上?
边上?(3)①求
 与
与 之间的函数关系式;
之间的函数关系式;②当
 取何值时,重叠部分的面积等于矩形面积的
取何值时,重叠部分的面积等于矩形面积的 ?
?
解:(1)如图, 四边形
四边形 是矩形,
是矩形, .
.
又 ,
, ,
, ,
,
 ,
, .
.
 ,
, .
.
 ,
, .
.
(2)如图1,

由轴对称的性质可知, ,
,
 ,
, .
.
由(1)知 ,
, ,
,
 ,
, .
.
 ,
, ,
, .
.
在 中,根据题意得:
中,根据题意得: ,
,
解这个方程得: .
.
(3)①当点 在矩形
在矩形 的内部或
的内部或 边上时,
边上时,
 ,
, ,
,
 ,
, 当
当 时,
时,
当 在矩形
在矩形 的外部时(如图2),
的外部时(如图2), ,
,

在 中,
中, ,
,
 ,
,
又 ,
, ,
,
在 中,
中,
 ,
, .
.
 ,
,
 ,
,
 当
当 时,
时, .
.
综上所述, 与
与 之间的函数解析式是:
之间的函数解析式是: .
.
②矩形面积 ,当
,当 时,函数
时,函数 随自变量的增大而增大,所以
随自变量的增大而增大,所以 的最大值是
的最大值是 ,而矩形面积的
,而矩形面积的 的值
的值 ,
,
而 ,所以,当
,所以,当 时,
时, 的值不可能是矩形面积的
的值不可能是矩形面积的 ;
;
当 时,根据题意,得:
时,根据题意,得:
 ,解这个方程,得
,解这个方程,得 ,因为
,因为 ,
,
所以 不合题意,舍去.
不合题意,舍去.
所以 .
.
综上所述,当 时,
时, 与矩形
与矩形 重叠部分的面积等于矩形面积的
重叠部分的面积等于矩形面积的 .
.
 四边形
四边形 是矩形,
是矩形, .
.又
 ,
, ,
, ,
, ,
, .
. ,
, .
. ,
, .
.(2)如图1,

由轴对称的性质可知,
 ,
, ,
, .
.由(1)知
 ,
, ,
, ,
, .
. ,
, ,
, .
.在
 中,根据题意得:
中,根据题意得: ,
,解这个方程得:
 .
.(3)①当点
 在矩形
在矩形 的内部或
的内部或 边上时,
边上时, ,
, ,
, ,
, 当
当 时,
时,
当
 在矩形
在矩形 的外部时(如图2),
的外部时(如图2), ,
,
在
 中,
中, ,
, ,
,又
 ,
, ,
,在
 中,
中, ,
, .
. ,
, ,
, 当
当 时,
时, .
.综上所述,
 与
与 之间的函数解析式是:
之间的函数解析式是: .
.②矩形面积
 ,当
,当 时,函数
时,函数 随自变量的增大而增大,所以
随自变量的增大而增大,所以 的最大值是
的最大值是 ,而矩形面积的
,而矩形面积的 的值
的值 ,
,而
 ,所以,当
,所以,当 时,
时, 的值不可能是矩形面积的
的值不可能是矩形面积的 ;
;当
 时,根据题意,得:
时,根据题意,得: ,解这个方程,得
,解这个方程,得 ,因为
,因为 ,
,所以
 不合题意,舍去.
不合题意,舍去.所以
 .
.综上所述,当
 时,
时, 与矩形
与矩形 重叠部分的面积等于矩形面积的
重叠部分的面积等于矩形面积的 .
.(1)利用PQ∥AC,Rt△ADC中,tan∠DAC= 从而得到角度;
从而得到角度;
(2)由折叠得△DPQ≌△EPQ,PE=x,PC= PE=
PE= x,再求出x;
x,再求出x;
利用三角形面积之间的关系求出,注意要分类讨论。
 从而得到角度;
从而得到角度;(2)由折叠得△DPQ≌△EPQ,PE=x,PC=
 PE=
PE= x,再求出x;
x,再求出x;利用三角形面积之间的关系求出,注意要分类讨论。

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 中,点
中,点 ,
, 分别是
分别是 的中点,
的中点, 分别是
分别是 的中点,
的中点, 满足什么条件时,四边形
满足什么条件时,四边形 是菱形?请证明你的结论.
是菱形?请证明你的结论.




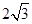
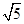




 的周长比
的周长比 的周长大7cm,则CD的长是 cm.
的周长大7cm,则CD的长是 cm.