Question

如图，已知AB=12；AB⊥BC于B，AB⊥AD于A，AD=5，BC=10．点E是CD的中点，则AE的长是

 

．

Answer 1

分析：首先作出辅助线连接DB，延长DA到F，使AD=AF，连接FC．根据三角形中位线定理可得AE=

1

2

CF，再利用勾股定理求出BD的长，然后证明可得到△FDC≌△BCD，从而得到FC=DB，进而得到答案．

解答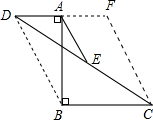：解：连接DB，延长DA到F，使AD=AF．连接FC，
∵AD=5，
∴AF=5，
∵点E是CD的中点，
∴AE=

1

2

CF，
在Rt△ABD中，
AD²+AB²=DB²，
∴BD=

52+122

=13，
∵AB⊥BC，AB⊥AD，
∴AD∥BC，
∴∠ADC=∠BCD，
又∵DF=BC，DC=DC，
∴△FDC≌△BCD，
∴FC=DB=13，
∴AE=

13

2

．
故答案为：

13

2

．

点评：此题主要考查了三角形中位线定理，勾股定理的综合运用，做题的关键是作出辅助线，证明BD=CF．