题目内容
 请观察如图,并回答下列问题:
请观察如图,并回答下列问题:(1)被测身高的学生有
36
36
人,(2)自左至右最后一组的频率是
| 1 |
| 12 |
| 1 |
| 12 |
(3)估计样本的中位数是多少?
163米
163米
(4)身高在160cm以上的有多少人?
23
23
占总人数的百分之几?(精确到0.1%)
63.9%
63.9%
.(5)在原图上画出频数分布折线图.
分析:(1)根据频数直方图直接得出被测身高的学生总数即可;
(2)根据自左至右最后一组的频数,求出频率即可;
(3)利用中位数的定义得出中位数的位置,进而估计样本的中位数即可;
(4)利用频数分布直方图得出身高在160cm以上的人数,进而得出所占百分比,
(5)利用频分布直方图直接得出折线图即可.
(2)根据自左至右最后一组的频数,求出频率即可;
(3)利用中位数的定义得出中位数的位置,进而估计样本的中位数即可;
(4)利用频数分布直方图得出身高在160cm以上的人数,进而得出所占百分比,
(5)利用频分布直方图直接得出折线图即可.
解答:解:(1)被测身高的学生有:4+9+12+8+3=36人.
故答案为:36;
(2)自左至右最后一组的频率是:
=
;
故答案为:
;
(3)根据样本总数为36,可知把数据从小到大排列后位于中间的数据是第18个和第19个的数据,
又因为第18个数据和第19个数据都落在第三组,
所以估计样本的中位数是163米,
故答案为:163米;
(4)身高在160cm以上的有:12+8+3=23人,
占总人数的:
×100%≈63.9%,
故答案为:23,63.9%;
(5)如图所示:

故答案为:36;
(2)自左至右最后一组的频率是:
| 3 |
| 36 |
| 1 |
| 12 |
故答案为:
| 1 |
| 12 |
(3)根据样本总数为36,可知把数据从小到大排列后位于中间的数据是第18个和第19个的数据,
又因为第18个数据和第19个数据都落在第三组,
所以估计样本的中位数是163米,
故答案为:163米;
(4)身高在160cm以上的有:12+8+3=23人,
占总人数的:
| 23 |
| 36 |
故答案为:23,63.9%;
(5)如图所示:

点评:本题考查了读频数分布直方图的能力和利用统计图获取信息的能力以及中位数定义等知识,利用频数分布直方图得出各组人数是解题关键.

练习册系列答案
相关题目
张师傅在铺地板时发现,用8块大小一样的长方形瓷砖恰好可以拼成一个大的长方形,如图1.然后,他用这8块瓷砖又拼出一个正方形,如图2,中间恰好空出一个边长为1的小正方形(阴影部分),假设长方形的长y,宽为x,且y>x.
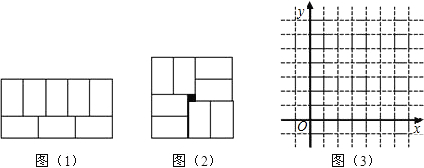
(1)请你求出图1中y与x的函数关系式;
(2)求出图2中y与x的函数关系式;
(3)在图3中作出两个函数的图象,写出交点坐标,并解释交点坐标的实际意义;
(4)根据以上讨论完成下表,观察x与y的关系,回答:如果给你任意8个相同的长方形,你能否拼成类似图1和图2的图形?说出你的理由.

(1)请你求出图1中y与x的函数关系式;
(2)求出图2中y与x的函数关系式;
(3)在图3中作出两个函数的图象,写出交点坐标,并解释交点坐标的实际意义;
(4)根据以上讨论完成下表,观察x与y的关系,回答:如果给你任意8个相同的长方形,你能否拼成类似图1和图2的图形?说出你的理由.
| 图(2)中小正方形边长 | 1 | 2 | 3 | 4 | … |
| x | 3 | 6 | 9 | 12 | … |
| y | 5 | 10 | 15 | 20 | … |
张师傅在铺地板时发现,用8块大小一样的长方形瓷砖恰好可以拼成一个大的长方形,如图1.然后,他用这8块瓷砖又拼出一个正方形,如图2,中间恰好空出一个边长为1的小正方形(阴影部分),假设长方形的长y,宽为x,且y>x.
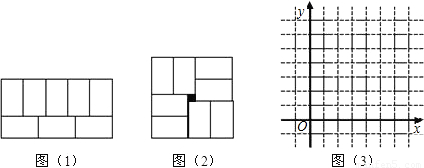
(1)请你求出图1中y与x的函数关系式;
(2)求出图2中y与x的函数关系式;
(3)在图3中作出两个函数的图象,写出交点坐标,并解释交点坐标的实际意义;
(4)根据以上讨论完成下表,观察x与y的关系,回答:如果给你任意8个相同的长方形,你能否拼成类似图1和图2的图形?说出你的理由.

(1)请你求出图1中y与x的函数关系式;
(2)求出图2中y与x的函数关系式;
(3)在图3中作出两个函数的图象,写出交点坐标,并解释交点坐标的实际意义;
(4)根据以上讨论完成下表,观察x与y的关系,回答:如果给你任意8个相同的长方形,你能否拼成类似图1和图2的图形?说出你的理由.
| 图(2)中小正方形边长 | 1 | 2 | 3 | 4 | … |
| x | 3 | 6 | 9 | 12 | … |
| y | 5 | 10 | 15 | 20 | … |
(2010•虹口区二模)下表是三峡水库2009年1-12月平均水位情况.小杰根据表1中的数据,在平面直角坐标系中以月份(月)为横坐标、月平均水位(米)为纵坐标描出了部分点(如图1),并绘制了不完整的频数分布直方图(如图2).请根据表1与图1、2中提供的信息,回答下列问题:
(1)根据表1,补全图1、图2;
(2)根据图1,可知平均水位相比其上个月平均水位上升最大的月份是______月;
(3)在2009年三峡水库1-12月各月的平均水位中,众数是______米,中位数是______米;
(4)观察图1中1-4月这些点的发展趋势,猜想1-4月y与x之间可以存在怎样的函数关系,请你用所学过的函数知识直接写出该函数关系式(不要求写定义域).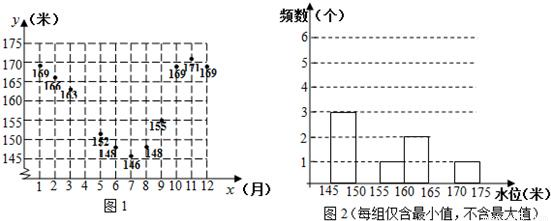
| 月份x(月) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 平均水位y(米) | 169 | 166 | 163 | 160 | 152 | 148 | 146 | 148 | 155 | 169 | 171 | 169 |
(2)根据图1,可知平均水位相比其上个月平均水位上升最大的月份是______月;
(3)在2009年三峡水库1-12月各月的平均水位中,众数是______米,中位数是______米;
(4)观察图1中1-4月这些点的发展趋势,猜想1-4月y与x之间可以存在怎样的函数关系,请你用所学过的函数知识直接写出该函数关系式(不要求写定义域).

(2010•新疆)张师傅在铺地板时发现,用8块大小一样的长方形瓷砖恰好可以拼成一个大的长方形,如图1.然后,他用这8块瓷砖又拼出一个正方形,如图2,中间恰好空出一个边长为1的小正方形(阴影部分),假设长方形的长y,宽为x,且y>x.

(1)请你求出图1中y与x的函数关系式;
(2)求出图2中y与x的函数关系式;
(3)在图3中作出两个函数的图象,写出交点坐标,并解释交点坐标的实际意义;
(4)根据以上讨论完成下表,观察x与y的关系,回答:如果给你任意8个相同的长方形,你能否拼成类似图1和图2的图形?说出你的理由.

(1)请你求出图1中y与x的函数关系式;
(2)求出图2中y与x的函数关系式;
(3)在图3中作出两个函数的图象,写出交点坐标,并解释交点坐标的实际意义;
(4)根据以上讨论完成下表,观察x与y的关系,回答:如果给你任意8个相同的长方形,你能否拼成类似图1和图2的图形?说出你的理由.
| 图(2)中小正方形边长 | 1 | 2 | 3 | 4 | … |
| x | 3 | 6 | 9 | 12 | … |
| y | 5 | 10 | 15 | 20 | … |

