题目内容
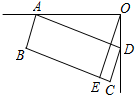 (2012•黄陂区模拟)如图是一台54英寸的大背投彩电放置在墙角的俯视图(其中ABCD是矩形).设∠ADO=α,彩电后背AD与前沿BC的距离为60cm,若AO=100cm,则墙角O到前沿BC的距离OE是( )
(2012•黄陂区模拟)如图是一台54英寸的大背投彩电放置在墙角的俯视图(其中ABCD是矩形).设∠ADO=α,彩电后背AD与前沿BC的距离为60cm,若AO=100cm,则墙角O到前沿BC的距离OE是( )分析:先根据直角三角形的性质得出∠ADO=∠AOF,再根据锐角三角函数的定义用AO与α表示出OF的长,进而可得出结论.
解答: 解:∵△AOD是直角三角形,
解:∵△AOD是直角三角形,
∴∠OAD+∠ODA=90°,
∵△AOF是直角三角形,
∴∠OAD+∠AOF=90°,
∴∠AOF=∠ADO=α,
在Rt△AOF中,OF=AO•cosα=100cosα,
∵EF=CD=60cm,
∴OE=EF+OF=(60+100cosα)cm.
故选B.
 解:∵△AOD是直角三角形,
解:∵△AOD是直角三角形,∴∠OAD+∠ODA=90°,
∵△AOF是直角三角形,
∴∠OAD+∠AOF=90°,
∴∠AOF=∠ADO=α,
在Rt△AOF中,OF=AO•cosα=100cosα,
∵EF=CD=60cm,
∴OE=EF+OF=(60+100cosα)cm.
故选B.
点评:本题考查的是解直角三角形的应用,根据题意得出∠AOF=∠ADO=α,再根据锐角三角函数的定义即可得出结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•黄陂区模拟)如图是一空心圆柱,其主视图正确的是( )
(2012•黄陂区模拟)如图是一空心圆柱,其主视图正确的是( )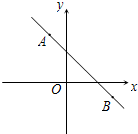 (2012•黄陂区模拟)如图,直线y=kx+b经过A(-1,3)、B(3,-1)两点,则不等式
(2012•黄陂区模拟)如图,直线y=kx+b经过A(-1,3)、B(3,-1)两点,则不等式 (2012•黄陂区模拟)如图,函数
(2012•黄陂区模拟)如图,函数 (2012•黄陂区模拟)如图,点B、C、D在一条直线上,AB⊥BC,ED⊥CD,∠1+∠2=90°.
(2012•黄陂区模拟)如图,点B、C、D在一条直线上,AB⊥BC,ED⊥CD,∠1+∠2=90°.