题目内容
2.(1)x2+2=x(2)(x-3)2+4x(x-3)=0.
分析 (1)公式法求解;
(2)因式分解法求解可得.
解答 解:(1)整理成一般式可得:x2-x+2=0,
∵a=1,b=-1,c=2,
∴△=(-1)2-4×1×2=-7<0,
∴方程无实数根;
(2)∵(x-3)(x-3+4x)=0,即(x-3)(5x-3)=0,
∴x-3=0或5x-3=0,
解得:x=3或x=$\frac{3}{5}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程右边变形为0,再把方程左边分解为两个一次式的乘积,这样原方程转化为两个一元一次方程,然后解一次方程即可得到一元二次方程的解..

练习册系列答案
相关题目
10.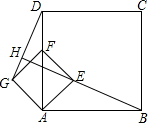 四边形ABCD、AEFG都是正方形,当正方形AEFG绕点A逆时针旋转45°时,如图,连接DG、BE,并延长BE交DG于点H,且BH⊥DG与H,若AB=4,AE=$\sqrt{2}$时,则线段BH的长是( )
四边形ABCD、AEFG都是正方形,当正方形AEFG绕点A逆时针旋转45°时,如图,连接DG、BE,并延长BE交DG于点H,且BH⊥DG与H,若AB=4,AE=$\sqrt{2}$时,则线段BH的长是( )
 四边形ABCD、AEFG都是正方形,当正方形AEFG绕点A逆时针旋转45°时,如图,连接DG、BE,并延长BE交DG于点H,且BH⊥DG与H,若AB=4,AE=$\sqrt{2}$时,则线段BH的长是( )
四边形ABCD、AEFG都是正方形,当正方形AEFG绕点A逆时针旋转45°时,如图,连接DG、BE,并延长BE交DG于点H,且BH⊥DG与H,若AB=4,AE=$\sqrt{2}$时,则线段BH的长是( )| A. | $4\sqrt{2}$ | B. | 16 | C. | $\frac{{8\sqrt{10}}}{5}$ | D. | $\frac{{3\sqrt{10}}}{2}$ |
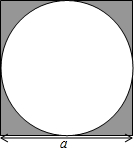 如图,一个边长为a的正方形内画了一个圆,其直径也是a
如图,一个边长为a的正方形内画了一个圆,其直径也是a 如图,E是正方形ABCD对角线BD上一点,EM⊥BC,EN⊥CD垂足分别是求M、N
如图,E是正方形ABCD对角线BD上一点,EM⊥BC,EN⊥CD垂足分别是求M、N 将长为30cm宽为10cm的长方形白纸,按如图方法粘合起来,粘合部分的宽度为3cm
将长为30cm宽为10cm的长方形白纸,按如图方法粘合起来,粘合部分的宽度为3cm 在纸面上有一数轴(如图所示),折叠纸面.
在纸面上有一数轴(如图所示),折叠纸面.