Question

【题目】阅读与应用：

阅读1：a、b为实数，且a＞0，b＞0，因为，所以，从而（当a＝b时取等号）．

阅读2：函数（常数m＞0，x＞0），由阅读1结论可知： ，所以当即时，函数的最小值为．

阅读理解上述内容，解答下列问题：

问题1：已知一个矩形的面积为4，其中一边长为x，则另一边长为，周长为，求当x＝__________时，周长的最小值为__________．

问题2：已知函数y1＝x＋1（x＞－1）与函数y2＝x2＋2x＋17（x＞－1），当x＝__________时， 的最小值为__________．

问题3：某民办学习每天的支出总费用包含以下三个部分：一是教职工工资6400元；二是学生生活费每人10元；三是其他费用．其中，其他费用与学生人数的平方成正比，比例系数为0.01．当学校学生人数为多少时，该校每天生均投入最低？最低费用是多少元？（生均投入＝支出总费用÷学生人数）

Answer 1

【答案】问题1： 2 8 问题2： 3 8 问题3：设学校学生人数为x人，生均投入为y元，依题意得： ，因为x＞0，所以，当即x=800时，y取最小值26．答：当学校学生人数为800人时，该校每天生均投入最低，最低费用是26元.

【解析】试题

问题1：当 时，周长有最小值，求x的值和周长最小值；

问题2：变形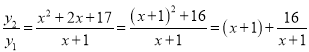，由当x+1= 时， 的最小值，求出x值和的最小值；

问题3：设学校学生人数为x人，生均投入为y元，根据生均投入=支出总费用÷学生人数，列出关系式，根据前两题解法，从而求解．

试题解析：

问题1：∵当 ( x>0)时，周长有最小值，

∴x=2，

∴当x=2时，有最小值为=4．即当x=2时，周长的最小值为2×4=8；

问题2：∵y1＝x＋1（x＞－1）与函数y2＝x2＋2x＋17（x＞－1），

∴，

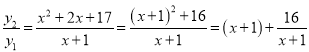∵当x+1= （x＞－1）时， 的最小值，

∴x=3，

∴x=3时， 有最小值为4+4＝8，即当x=3时， 的最小值为8；

问题3：设学校学生人数为x人，则生均投入y元，依题意得

，因为x＞0，所以，当即x=800时，y取最小值26.

答：当学校学生人数为800时，该校每天生均投入最低，最低费用是26元．