题目内容
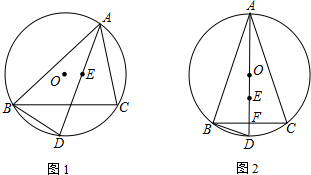
18. 如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD、BE、CE,若∠CBD=32°,则∠BEC的度数为122°.
如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD、BE、CE,若∠CBD=32°,则∠BEC的度数为122°.
分析 根据圆周角定理可求∠CAD=32°,再根据三角形内心的定义可求∠BAC,再根据三角形内角和定理和三角形内心的定义可求∠EBC+∠ECB,再根据三角形内角和定理可求∠BEC的度数.
解答 解:在⊙O中,∵∠CBD=32°,
∵∠CAD=32°,
∵点E是△ABC的内心,
∴∠BAC=64°,
∴∠EBC+∠ECB=(180°-64°)÷2=58°,
∴∠BEC=180°-58°=122°.
故答案为:122°.
点评 考查了三角形的内切圆与内心,圆周角定理,三角形内角和定理,关键是得到∠EBC+∠ECB的度数.

练习册系列答案
相关题目
8.已知关于x的一元二次方程x2+mx-8=0的一个实数根为2,则另一实数根及m的值分别为( )
| A. | 4,-2 | B. | -4,-2 | C. | 4,2 | D. | -4,2 |
9.二次函数y=x2-2x+4化为y=a(x-h)2+k的形式,下列正确的是( )
| A. | y=(x-1)2+2 | B. | y=(x-1)2+3 | C. | y=(x-2)2+2 | D. | y=(x-2)2+4 |


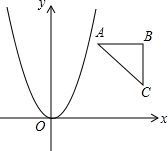 已知Rt△ABC的顶点坐标为A(1,2),B(2,2),C(2,1),若抛物线y=ax2与该直角三角形无公共点,则a的取值范围是a<0或a>2或0<a<$\frac{1}{4}$.
已知Rt△ABC的顶点坐标为A(1,2),B(2,2),C(2,1),若抛物线y=ax2与该直角三角形无公共点,则a的取值范围是a<0或a>2或0<a<$\frac{1}{4}$.