题目内容
【题目】在矩形ABCD中,有一个菱形BFDE(点E,F分别在线段AB,CD上),记它们的面积分别为SABCD和SBFDE , 现给出下列命题:①若 ![]() =
= ![]() ,则tan∠EDF=
,则tan∠EDF= ![]() ;②若DE2=BDEF,则DF=2AD,则( )
;②若DE2=BDEF,则DF=2AD,则( ) 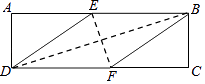
A.①是假命题,②是假命题
B.①是真命题,②是假命题
C.①是假命题,②是真命题
D.①是真命题,②是真命题
【答案】D
【解析】解:①设CF=x,DF=y,BC=h. ∵四边形BFDE是菱形,
∴BF=DF=y,DE∥BF.
∵若 ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,即cos∠BFC=
,即cos∠BFC= ![]() ,
,
∴∠BFC=30°,
∵DE∥BF,
∴∠EDF=∠BFC=30°,
∴tan∠EDF= ![]() ,
,
所以①是真命题.
②∵四边形BFDE是菱形,
∴DF=DE.
∵S△DEF= ![]() DFAD=
DFAD= ![]() BDEF,
BDEF,
又∵DE2=BDEF(已知),
∴S△DEF= ![]() DE2=
DE2= ![]() DF2 ,
DF2 ,
∴DFAD= ![]() DF2 ,
DF2 ,
∴DF=2AD,
所以②是真命题.
故选D.
【考点精析】解答此题的关键在于理解菱形的性质的相关知识,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.

练习册系列答案
相关题目