题目内容
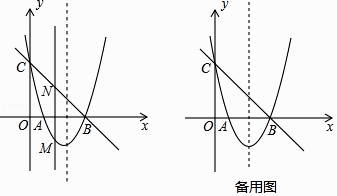
【题目】如图，在平面直角坐标系中，抛物线y=ax2+6x+c（a≠0）交y轴于A点，交x轴于B、C两点（点B在点C的左侧），已知A点坐标为（0，﹣5），点B的坐标为（1，0）．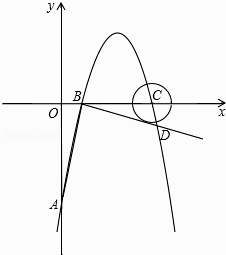
（1）求此抛物线的解析式及定点坐标；
（2）过点B作线段AB的垂线交抛物线于点D，如果以点C为圆心的圆与直线BD相切，请判断抛物线的对称轴与⊙C的位置关系，并说明理由；
（3）在抛物线上是否存在一点P，使△ACP是以AC为直角边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．
【答案】
（1）
解：把A（0，﹣5），B（1，0）代入y=ax2+6x+c得 
，解得 
，
∴抛物线解析式为y=﹣x2+6x﹣5，
∵y=﹣（x﹣3）2+4，
∴抛物线的顶点坐标为（3，4）；
（2）
解：抛物线的对称轴与⊙C相离．理由如下：
当y=0时，﹣x2+6x﹣5=0，解得x1=1，x2=5，则C（5，0），
∴BC=4，
在Rt△OAB中，AB= 
= 
，
作CE⊥BD于E点，如图1，
∵AB⊥BD，
∴∠ABO+∠CBE=90°，
而∠ABO+∠BAO=90°，
∴∠BAO=∠CBE，
∴Rt△ABO∽Rt△BCE，
∴ 
= 
，即 
= 
，
∴CE= 
，
∵⊙C与BD相切，
∴⊙C的半径为 ，
∵点C到对称轴x=3的距离为2，
而2＞ ，
∴抛物线的对称轴与⊙C相离；
（3）
解：存在．
（I）当∠PCA=90°时，如图3，CP交y轴于Q，
∵A（0，﹣5），C（5，0），
∴△AOC为等腰直角三角形，∠OCA=45°；
∵PC⊥AC，
∴∠PCO=45°，
∴△OCQ为等腰直角三角形，
∴OQ=OC=5，
∴Q（0，5），
易得直线CQ的解析式为y=﹣x+5，
解方程组 
得 
或 
，此时点P坐标为（2，3）；
（II）当∠PAC=90°时，如图4，过点P作PF⊥y轴于点F，
∵A（0，﹣5），C（5，0），
∴△AOC为等腰直角三角形，∠OAC=45°；
∵PA⊥AC，
∴∠PAF=45°，即△PAF为等腰直角三角形．
设点P坐标为（t，﹣t2+6t﹣5），
∵AF=PF，
∴﹣5﹣（﹣t2+6t﹣5）=t解得t=0或t=7，此时点P坐标为（7，﹣12），
综上所述，存在点P，使△ACP是以AC为直角边的直角三角形．点P的坐标为（2，3）或（7，﹣12）．
【解析】（1）把A（0，﹣5），B（1，0）代入y=ax2+6x+c得关于a、c的方程组，然后解方程组即可，再把解析式配成顶点式即可得到抛物线的顶点坐标；（2）先解方程﹣x2+6x﹣5=0得C（5，0），则BC=4，再利用勾股定理计算出AB= ，作CE⊥BD于E点，如图1，证明Rt△ABO∽Rt△BCE，利用相似比可计算出CE= ，则根据切线的性质得⊙C的半径为 ，然后根据直线与圆的位置关系的判定方法判断抛物线的对称轴与⊙C的位置关系；（3）讨论：当∠PCA=90°时，如图3，CP交y轴于Q，利用△AOC为等腰直角三角形可得到△OCQ为等腰直角三角形，则直线CQ的解析式为y=﹣x+5，于是解方程组 得此时点P坐标；当∠PAC=90°时，如图4，过点P作PF⊥y轴于点F，利用△AOC为等腰直角三角形得到△PAF为等腰直角三角形．设点P坐标为（t，﹣t2+6t﹣5），则﹣5﹣（﹣t2+6t﹣5）=t，然后解方程求出t即可得到此时点P坐标．
