题目内容
已知关于x的方程2x2-mx-2m+1=0的两根x1，x2，且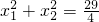
，试求m的值．
解：由题意：x1+x2=
，x1•x2=
，
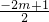∵x12+x22=
，
∴（x1+x2）2-2x1•x2=，
即（）2-2×=，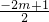
整理得：m2+8m-33=0，
即（m+11）（m-3）=0，
解得m1=-11，m2=3，
当m=-11时，△=m2-4×2（1-2m）=-63＜0，
当m=3时，△=m2-4×2（1-2m）=49＞0，
所以，m=3．
分析：利用根与系数的关系求出x1+x2，x1•x2，再根据完全平方公式整理得到关于m的方程，求解，再代入根的判别式△进行验证即可得解．
点评：本题考查了根与系数的关系，利用根与系数的关系把根的方程转化为关于m的方程是解题的关键，要注意利用根的判别式验证所求的m的值．
，x1•x2=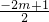，∵x12+x22=
，∴（x1+x2）2-2x1•x2=
，即（
）2-2×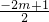=，整理得：m2+8m-33=0，
即（m+11）（m-3）=0，
解得m1=-11，m2=3，
当m=-11时，△=m2-4×2（1-2m）=-63＜0，
当m=3时，△=m2-4×2（1-2m）=49＞0，
所以，m=3．
分析：利用根与系数的关系求出x1+x2，x1•x2，再根据完全平方公式整理得到关于m的方程，求解，再代入根的判别式△进行验证即可得解．
点评：本题考查了根与系数的关系，利用根与系数的关系把根的方程转化为关于m的方程是解题的关键，要注意利用根的判别式验证所求的m的值．
练习册系列答案
相关题目
已知关于x的方程2x-3=
+x的解满足|x|=1，则m的值是（ ）
| m |
| 3 |
| A、-6 | B、-12 |
| C、-6或-12 | D、6或12 |