题目内容
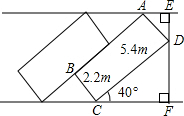（2012•重庆模拟）如图，矩形ABCD是一辆机动车停放的车位示意图，请根据图中数据，计算车位所占街道的宽度EF约为5.2m
5.2m
．（结果保留两位有效数字，参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84）分析：求EF的长，只要求出ED，DF即可．直角三角形CDF中已知了∠DCF的度数，已知CD的长DF就很容易求出了，同理可求出DE的长，DF+DE就是EF的长．
解答：解：在Rt△CFD中DF=CD•sin40°≈5.4×0.64=3.456．
∵四边形ABCD是矩形．
∴∠ADC=90°．
∵∠CDF=90°-40°=50°．
∴∠ADE=180°-90°-50°=40°．
在Rt△DAE中DE=AD•cos40°≈2.2×0.77=1.694．
∴EF=DF+DE=3.456+1.694≈5.2（m）．
故答案为：5.2m．
∵四边形ABCD是矩形．
∴∠ADC=90°．
∵∠CDF=90°-40°=50°．
∴∠ADE=180°-90°-50°=40°．
在Rt△DAE中DE=AD•cos40°≈2.2×0.77=1.694．
∴EF=DF+DE=3.456+1.694≈5.2（m）．
故答案为：5.2m．
点评：本题是将实际问题转化为直角三角形中的数学问题，可把条件和问题放到直角三角形中，进行解决．
练习册系列答案
相关题目