题目内容
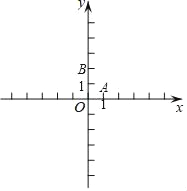
【题目】已知在平面直角坐标系xOy（如图）中，已知抛物线y=
+bx+c点经过A（1，0）、B（0，2）．
（1）求该抛物线的表达式；
（2）设该抛物线的对称轴与x轴的交点为C，第四象限内的点D在该抛物线的对称轴上，如果以点A、C、D所组成的三角形与△AOB相似，求点D的坐标；
（3）设点E在该抛物线的对称轴上，它的纵坐标是1，联结AE、BE，求sin∠ABE．
【答案】（1）y=
x+2．（2）点D的坐标为（2，﹣
）或（2，﹣2）；（3）
.
【解析】试题分析：（1）运用待定系数法求出抛物线的解析式为
；
（2）以点
、
、
所组成的三角形与△
相似有两种：①当
时， 
，可求得点
的坐标为
；②当
时，同理求出
，点
的坐标为
；
（3）先由勾股定理求出BE的长，再通过计算求出
，过点
作
，利用面积求出BE的长，在Rt△
中即可求出
的值.
试题解析：（1）∵抛物线
点经过
、
∴
∴
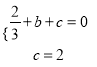
∴抛物线的表达式是
（2）由（1）得： 
的对称轴是直线
∴点
的坐标为
，
∵第四象限内的点
在该抛物线的对称轴上
∴以点
、
、
所组成的三角形与△
相似有两种
①当
时， 
，
∴
， 
∴点
的坐标为
②当
时，同理求出
∴点
的坐标为
综上所述，点
的坐标为
或
（3）∵点
在该抛物线的对称轴直线
上，且纵坐标是
∴点
坐标是
，
又点
，
∴
设直线
与
轴的交点仍是点
∴
∴
过点
作
，垂足为点
, 
∴
∴
在Rt△
中， 
∴
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
