题目内容
如图，已知AB是⊙O的直径，弦AC平分∠DAB，CD⊥AD于D．则CD是⊙O的切线吗？请说明理由．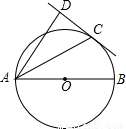
【答案】分析：连接OC，只要证明OC⊥CD即可．
解答：
解：CD是⊙O的切线．
理由如下：（1分）
连接OC；
∵OA=OC，
∴∠CAO=∠OCA，（1分）
∵∠DAC=∠CAO，
∴∠DAC=∠OCA，（2分）
∴AD∥OC（2分）；
又∵CD⊥AD，
∴OC⊥CD，（2分）
∴CD是⊙O的切线．（1分）
点评：本题考查的是切线的判定，要证某线是圆的切线，已知此线过圆上某点，连接圆心和这点（即为半径），再证垂直即可．
解答：
解：CD是⊙O的切线．理由如下：（1分）
连接OC；
∵OA=OC，
∴∠CAO=∠OCA，（1分）
∵∠DAC=∠CAO，
∴∠DAC=∠OCA，（2分）
∴AD∥OC（2分）；
又∵CD⊥AD，
∴OC⊥CD，（2分）
∴CD是⊙O的切线．（1分）
点评：本题考查的是切线的判定，要证某线是圆的切线，已知此线过圆上某点，连接圆心和这点（即为半径），再证垂直即可．
练习册系列答案
暑假作业海燕出版社系列答案
相关题目
如图，已知AB是⊙O的直径，AC是弦，D为AB延长线上一点，DC=AC，∠ACD=120°，BD=10．
如图，已知AB是⊙O的直径，C是⊙O上一点，∠BAC的平分线交⊙O于点D，交⊙O的切线BE于点E，过点D作DF⊥AC，交AC的延长线于点F．
（2013•泰安）如图，已知AB是⊙O的直径，AD切⊙O于点A，点C是
如图，已知AB是⊙O的直径，P为⊙O外一点，且OP∥BC，∠P=∠BAC．
如图，已知AB是圆O的直径，∠DAB的平分线AC交圆O与点C，作CD⊥AD，垂足为点D，直线CD与AB的延长线交于点E．