题目内容
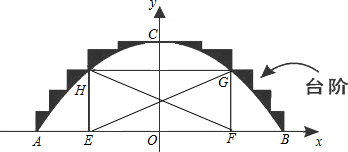
某公园有一个抛物线形状的观景拱桥ABC,其横截面如图所示,在图中建立的直角坐标系中,抛物线的解析式为y=-| 1 | 20 |
(1)现因搞庆典活动,计划沿拱桥的台阶表面铺设一条宽度为1.5m的地毯,地毯的价格为20元/m2,求购买地毯需多少元?
(2)在拱桥加固维修时,搭建的“脚手架”为矩形EFGH(H、G分别在抛物线的左右侧上),并增加铺设斜面EG和HF,已知矩形EFGH的周长为27.5m,求增加斜面的长.
分析:(1)求出抛物线与x轴交点的坐标,AB的长度即可求得,再由已知顶点C的坐标,根据平移的性质求得地毯的总长度,进一步求得面积解决问题;
(2)设出抛物线点G的坐标,分别表示出矩形的长和宽,并利用矩形的周长求得长和宽,进一步利用矩形的性质及勾股定理解答问题.
(2)设出抛物线点G的坐标,分别表示出矩形的长和宽,并利用矩形的周长求得长和宽,进一步利用矩形的性质及勾股定理解答问题.
解答:解:(1)因为顶点C(0,5),c=5,所以OC=5,
令y=0,即-
x2+5=0,
解得x1=10,x2=-10,
∴AB=10-(-10)=20,
∴地毯的总长度为:AB+2OC=20+2×5=30,
∴30×1.5×20=900(元).
答:购买地毯需要900元.
(2)设G的坐标为(m,-
m2+5),其中m>0,
则EF=2m,GF=-
m2+5.
由已知得:2(EF+GF)=27.5,
即2(2m-
m2+5)=27.5,
解得:m1=5,m2=35(不合题意,舍去),
把m1=5代入-
m2+5=-
×52+5=3.75.
∴点G的坐标是(5,3.75).
∴EF=10,GF=3.75;
∴EG=
=
=
,
又∵EG=HF,
∴EG+HF=
.
答:斜面的长为
.
令y=0,即-
| 1 |
| 20 |
解得x1=10,x2=-10,
∴AB=10-(-10)=20,
∴地毯的总长度为:AB+2OC=20+2×5=30,
∴30×1.5×20=900(元).
答:购买地毯需要900元.
(2)设G的坐标为(m,-
| 1 |
| 20 |
则EF=2m,GF=-
| 1 |
| 20 |
由已知得:2(EF+GF)=27.5,
即2(2m-
| 1 |
| 20 |
解得:m1=5,m2=35(不合题意,舍去),
把m1=5代入-
| 1 |
| 20 |
| 1 |
| 20 |
∴点G的坐标是(5,3.75).
∴EF=10,GF=3.75;
∴EG=
| EF2+FG2 |
| 102+3.752 |
5
| ||
| 4 |
又∵EG=HF,
∴EG+HF=
5
| ||
| 2 |
答:斜面的长为
5
| ||
| 2 |
点评:此题主要考查二次函数图象与坐标轴交点坐标,矩形的性质,勾股定理,是一道数形结合的好题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
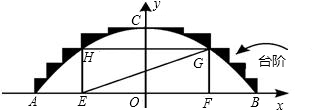

 某公园有一个抛物线形状的观景拱桥ABC,其横截面如图所示,量得该拱桥占地面最宽处AB=20米,最高处点C距地面5米(即OC=5米)
某公园有一个抛物线形状的观景拱桥ABC,其横截面如图所示,量得该拱桥占地面最宽处AB=20米,最高处点C距地面5米(即OC=5米) (3)在拱桥加固维修时,搭建的“脚手架”为矩形EFGH(H、G分别在抛物线的左右侧上),并铺设斜面EG.已知矩形EFGH的周长为27.5 m,求斜面EG的倾斜角∠GEF的正切值.
(3)在拱桥加固维修时,搭建的“脚手架”为矩形EFGH(H、G分别在抛物线的左右侧上),并铺设斜面EG.已知矩形EFGH的周长为27.5 m,求斜面EG的倾斜角∠GEF的正切值.