题目内容
11、如图，点D是等腰直角△ABC斜边AB上的点，将△ACD绕点C逆时针旋转，使它与△BCD′重合，则∠D′BA=90
度．分析：根据旋转的性质，△ACD≌△BCD′，∠A=∠CBD′，因为△ABC为等腰直角三角形，所以∠A+∠CBD=90°，从而得出∠CBA+∠CBD′=90°，即可得出结论．
解答：解：根据旋转的性质，
得出：△ACD≌△BCD′，
∴∠A=∠CBD′，
∵△ABC为等腰直角三角形，
∴∠A+∠CBD=90°，
∴∠D′BA=∠CBD+∠CBD′=90°．
故答案为90°．
得出：△ACD≌△BCD′，
∴∠A=∠CBD′，
∵△ABC为等腰直角三角形，
∴∠A+∠CBD=90°，
∴∠D′BA=∠CBD+∠CBD′=90°．
故答案为90°．
点评：本题主要考查了旋转的性质：①对应点到旋转中心的距离相等，②对应点与旋转中心所连线段的夹角等于旋转角，③旋转前、后的图形全，同时考查了等腰直角三角形的性质，难度适中．
练习册系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
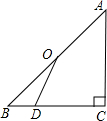已知：如图，点O是等腰直角△ABC斜边AB的中点，D为BC边上任意一点．
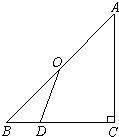27、附加题：已知：如图，点O是等腰直角△ABC斜边AB的中点，D为BC边上任意一点．
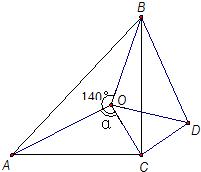28、如图，点O是等腰直角三角形ABC内一点，∠ACB=90°，∠AOB=140°，∠AOC=α．将△AOC绕直角顶点C按顺时针方向旋转90°得△BDC，连接OD．
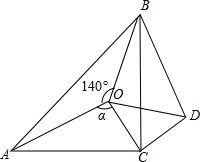AOC绕直角顶点C按顺时针方向旋转90°得△BDC，连接OD．