题目内容
如图，在?ABCD中，点E在边AD上，以BE为折痕将△ABE向上翻折，点A正好落在CD的点F处，若△FDE的周长为8，△FCB的周长为22，则?ABCD的周长为________．
30
分析：根据折叠的性质可得EF=AE、BF=BA，从而?ABCD的周长可转化为：△FDE的周长+△FCB的周长，结合题意条件即可得出答案．
解答：由折叠的性质可得EF=AE、BF=BA，
∴?ABCD的周长=DF+FC+CB+BA+AE+DE=△FDE的周长+△FCB的周长=30．
故答案为：30．
点评：此题考查了折叠的性质，难度一般，关键是根据折叠的性质得出EF=AE、BF=BA，将平行四边形的周长进行转化，难度一般．
分析：根据折叠的性质可得EF=AE、BF=BA，从而?ABCD的周长可转化为：△FDE的周长+△FCB的周长，结合题意条件即可得出答案．
解答：由折叠的性质可得EF=AE、BF=BA，
∴?ABCD的周长=DF+FC+CB+BA+AE+DE=△FDE的周长+△FCB的周长=30．
故答案为：30．
点评：此题考查了折叠的性质，难度一般，关键是根据折叠的性质得出EF=AE、BF=BA，将平行四边形的周长进行转化，难度一般．
练习册系列答案
阅读快车系列答案
相关题目
如图，在?ABCD中，对角线AC、BD相交于点O，AB=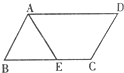
18、如图，在?ABCD中，∠A的平分线交BC于点E，若AB=10cm，AD=14cm，则EC=
（2011•犍为县模拟）甲题：已知关于x的一元二次方程x2=2（1-m）x-m2的两实数根为x1，x2．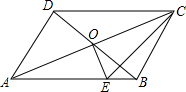
如图，在?ABCD中，∠ADB=90°，CA=10，DB=6，OE⊥AC于点O，连接CE，则△CBE的周长是