Question

如图，△ACB中，∠A=90°，BC=2，分别以B，C为圆心的等圆⊙B，⊙C外切，则两圆中阴影扇形的面积之和为________．

Answer 1

π
分析：由等圆⊙B，⊙C外切，BC=2，即可求得⊙B，⊙C的半径为1，又由△ACB中，∠A=90°，即可得∠B+∠C=90°，然后根据扇形的面积的求解方法求解即可求得答案．
解答：∵等圆⊙B，⊙C外切，BC=2，
∴⊙B，⊙C的半径为1，
∵△ACB中，∠A=90°，
∴∠B+∠C=90°，
∴两圆中阴影扇形的面积之和为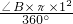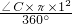：+=π×（∠B+∠C）=π．
故答案为：π．
点评：此题考查了相切两圆的性质、扇形的面积以及直角三角形的性质．此题难度不大，注意掌握数形结合思想与整体思想的应用．