题目内容
在平面直角坐标系xOy中,直线y=kx(k为常数)与抛物线y= x2-2交于A,B两点,且A点在y轴左侧,P点的坐标为(0,-4),连接PA,PB.有以下说法:
x2-2交于A,B两点,且A点在y轴左侧,P点的坐标为(0,-4),连接PA,PB.有以下说法:
①PO2=PA•PB;
②当k>0时,(PA+AO)(PB-BO)的值随k的增大而增大;
③当k= 时,BP2=BO•BA;
时,BP2=BO•BA;
④△PAB面积的最小值为 .
.
其中正确的是________.(写出所有正确说法的序号)
③④
分析:首先得到两个基本结论:
(I)设A(m,km),B(n,kn),联立两个解析式,由根与系数关系得到:m+n=3k,mn=-6;
(II)直线PA、PB关于y轴对称.
利用以上结论,解决本题:
(1)说法①错误.如答图1,设点A关于y轴的对称点为A′,若结论①成立,则可以证明△POA′∽△PBO,得到∠AOP=∠PBO.而∠AOP是△PBO的外角,∠AOP>∠PBO,由此产生矛盾,故说法①错误;
(2)说法②错误.如答图2,可求得(PA+AO)(PB-BO)=16为定值,故错误;
(3)说法③正确.联立方程组,求得点A、B坐标,进而求得BP、BO、BA,验证等式BP2=BO•BA成立,故正确;
(4)说法④正确.由根与系数关系得到:S△PAB=2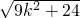 ,当k=0时,取得最小值为
,当k=0时,取得最小值为 ,故正确.
,故正确.
解答:设A(m,km),B(n,kn),其中m<0,n>0.
联立y= x2-2与y=kx得:
x2-2与y=kx得: x2-2=kx,即x2-3kx-6=0,
x2-2=kx,即x2-3kx-6=0,
∴m+n=3k,mn=-6.
设直线PA的解析式为y=ax+b,将P(0,-4),A(m,km)代入得:
 ,解得a=
,解得a=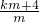 ,b=-4,
,b=-4,
∴y=(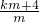 )x-4.
)x-4.
令y=0,得x= ,
,
∴直线PA与x轴的交点坐标为( ,0).
,0).
同理可得,直线PB的解析式为y=( )x-4,直线PB与x轴交点坐标为(
)x-4,直线PB与x轴交点坐标为(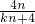 ,0).
,0).
∵ +
+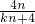 =
=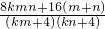 =
= =0,
=0,
∴直线PA、PB与x轴的交点关于y轴对称,即直线PA、PB关于y轴对称.
(1)说法①错误.理由如下:
如答图1所示,∵PA、PB关于y轴对称,
∴点A关于y轴的对称点A′落在PB上.
连接OA′,则OA=OA′,∠POA=∠POA′.
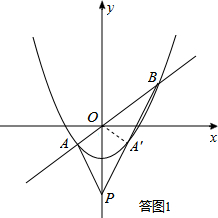
假设结论:PO2=PA•PB成立,即PO2=PA′•PB,
∴ ,
,
又∵∠BPO=∠BPO,
∴△POA′∽△PBO,
∴∠POA′=∠PBO,
∴∠AOP=∠PBO.
而∠AOP是△PBO的外角,
∴∠AOP>∠PBO,矛盾,
∴说法①错误.
(2)说法②错误.理由如下:
易知: =-
=- ,
,
∴OB=- OA.
OA.
由对称可知,PO为△APB的角平分线,
∴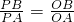 ,
,
∴PB=- PA.
PA.
∴(PA+AO)(PB-BO)=(PA+AO)[- PA-(-
PA-(- OA)]=-
OA)]=- (PA+AO)(PA-OA)=-
(PA+AO)(PA-OA)=- (PA2-AO2).
(PA2-AO2).
如答图2所示,过点A作AD⊥y轴于点D,则OD=-km,PD=4+km.

∴PA2-AO2=(PD2+AD2)-(OD2+AD2)=PD2-OD2=(4+km)2-(-km)2=8km+16,
∵m+n=3k,∴k= (m+n),
(m+n),
∴PA2-AO2=8• (m+n)•m+16=
(m+n)•m+16= m2+
m2+ mn+16=
mn+16= m2+
m2+ ×(-6)+16=
×(-6)+16= m2.
m2.
∴(PA+AO)(PB-BO)=- (PA2-AO2)=-
(PA2-AO2)=- •
• m2=-
m2=- mn=-
mn=- ×(-6)=16.
×(-6)=16.
即:(PA+AO)(PB-BO)为定值,所以说法②错误.
(3)说法③正确.理由如下:
当k= 时,联立方程组:
时,联立方程组: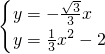 ,得A(
,得A(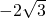 ,2),B(
,2),B( ,-1),
,-1),
∴BP2=12,BO•BA=2×6=12,
∴BP2=BO•BA,故说法③正确.
(4)说法④正确.理由如下:
S△PAB=S△PAO+S△PBO= OP•(-m)+
OP•(-m)+ OP•n=
OP•n= OP•(n-m)=2(n-m)=2
OP•(n-m)=2(n-m)=2 =2
=2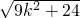 ,
,
∴当k=0时,△PAB面积有最小值,最小值为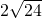 =
= .
.
故说法④正确.
综上所述,正确的说法是:③④.
故答案为:③④.
点评:本题是代数几何综合题,难度很大.解答中首先得到两个基本结论,其中PA、PB的对称性是判定说法①的基本依据,根与系数关系的结论是判定说法②、④的关键依据.正确解决本题的关键是打好数学基础,将平时所学知识融会贯通、灵活运用.
分析:首先得到两个基本结论:
(I)设A(m,km),B(n,kn),联立两个解析式,由根与系数关系得到:m+n=3k,mn=-6;
(II)直线PA、PB关于y轴对称.
利用以上结论,解决本题:
(1)说法①错误.如答图1,设点A关于y轴的对称点为A′,若结论①成立,则可以证明△POA′∽△PBO,得到∠AOP=∠PBO.而∠AOP是△PBO的外角,∠AOP>∠PBO,由此产生矛盾,故说法①错误;
(2)说法②错误.如答图2,可求得(PA+AO)(PB-BO)=16为定值,故错误;
(3)说法③正确.联立方程组,求得点A、B坐标,进而求得BP、BO、BA,验证等式BP2=BO•BA成立,故正确;
(4)说法④正确.由根与系数关系得到:S△PAB=2
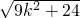 ,当k=0时,取得最小值为
,当k=0时,取得最小值为 ,故正确.
,故正确.解答:设A(m,km),B(n,kn),其中m<0,n>0.
联立y=
 x2-2与y=kx得:
x2-2与y=kx得: x2-2=kx,即x2-3kx-6=0,
x2-2=kx,即x2-3kx-6=0,∴m+n=3k,mn=-6.
设直线PA的解析式为y=ax+b,将P(0,-4),A(m,km)代入得:
 ,解得a=
,解得a=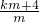 ,b=-4,
,b=-4,∴y=(
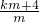 )x-4.
)x-4.令y=0,得x=
 ,
,∴直线PA与x轴的交点坐标为(
 ,0).
,0).同理可得,直线PB的解析式为y=(
 )x-4,直线PB与x轴交点坐标为(
)x-4,直线PB与x轴交点坐标为(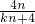 ,0).
,0).∵
 +
+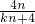 =
=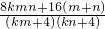 =
= =0,
=0,∴直线PA、PB与x轴的交点关于y轴对称,即直线PA、PB关于y轴对称.
(1)说法①错误.理由如下:
如答图1所示,∵PA、PB关于y轴对称,
∴点A关于y轴的对称点A′落在PB上.
连接OA′,则OA=OA′,∠POA=∠POA′.

假设结论:PO2=PA•PB成立,即PO2=PA′•PB,
∴
 ,
,又∵∠BPO=∠BPO,
∴△POA′∽△PBO,
∴∠POA′=∠PBO,
∴∠AOP=∠PBO.
而∠AOP是△PBO的外角,
∴∠AOP>∠PBO,矛盾,
∴说法①错误.
(2)说法②错误.理由如下:
易知:
 =-
=- ,
,∴OB=-
 OA.
OA.由对称可知,PO为△APB的角平分线,
∴
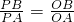 ,
,∴PB=-
 PA.
PA.∴(PA+AO)(PB-BO)=(PA+AO)[-
 PA-(-
PA-(- OA)]=-
OA)]=- (PA+AO)(PA-OA)=-
(PA+AO)(PA-OA)=- (PA2-AO2).
(PA2-AO2).如答图2所示,过点A作AD⊥y轴于点D,则OD=-km,PD=4+km.

∴PA2-AO2=(PD2+AD2)-(OD2+AD2)=PD2-OD2=(4+km)2-(-km)2=8km+16,
∵m+n=3k,∴k=
 (m+n),
(m+n),∴PA2-AO2=8•
 (m+n)•m+16=
(m+n)•m+16= m2+
m2+ mn+16=
mn+16= m2+
m2+ ×(-6)+16=
×(-6)+16= m2.
m2.∴(PA+AO)(PB-BO)=-
 (PA2-AO2)=-
(PA2-AO2)=- •
• m2=-
m2=- mn=-
mn=- ×(-6)=16.
×(-6)=16.即:(PA+AO)(PB-BO)为定值,所以说法②错误.
(3)说法③正确.理由如下:
当k=
 时,联立方程组:
时,联立方程组: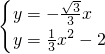 ,得A(
,得A(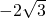 ,2),B(
,2),B( ,-1),
,-1),∴BP2=12,BO•BA=2×6=12,
∴BP2=BO•BA,故说法③正确.
(4)说法④正确.理由如下:
S△PAB=S△PAO+S△PBO=
 OP•(-m)+
OP•(-m)+ OP•n=
OP•n= OP•(n-m)=2(n-m)=2
OP•(n-m)=2(n-m)=2 =2
=2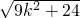 ,
,∴当k=0时,△PAB面积有最小值,最小值为
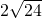 =
= .
.故说法④正确.
综上所述,正确的说法是:③④.
故答案为:③④.
点评:本题是代数几何综合题,难度很大.解答中首先得到两个基本结论,其中PA、PB的对称性是判定说法①的基本依据,根与系数关系的结论是判定说法②、④的关键依据.正确解决本题的关键是打好数学基础,将平时所学知识融会贯通、灵活运用.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点. 如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为
如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为