题目内容
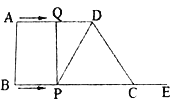
【题目】AC是□ABCD的一条对角线，过AC中点O的直线分别交AD、BC 于点E、F.
（1）求证：AE=CF；
（2）连接AF，CE.
①当EF⊥AC时，四边形AFCE是什么四边形？请证明你的结论；
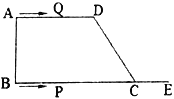
②若AB=1，BC=2，∠B=60°，则四边形AFCE为矩形时，求EF的长.
【答案】（1）证明见解析；（2）①菱形，证明见解析，②
【解析】试题分析：（1）由平行四边形的性质可知OA=OC，∠AEO=∠OFC，∠EAO=∠OCF，证出△AOE≌△COF，即可得出AE=CF．
（2）①先证明四边形AFCE是平行四边形，由EF⊥AC，即可得出四边形AFCE是菱形；
②由矩形的性质得出EF=AC，∠AFB=∠AFC=90°，求出AF、CF，由勾股定理求出AC，即可得出EF的长．
试题解析：（1）∵O是AC中点
∴AO=C0
∵ABCD是平行四边形
∴AD∥BC
∴∠DAC=∠BCA
在ΔAOE和ΔCOF中
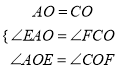
∴ΔAOE ≌ ΔCOF(ASA)
∴AE=CF
（2）①菱形
∵AE∥CF且AE=CF
∴AECF是平行四边形
∵AC⊥EF
∴AECF是菱形
②∵AECF是矩形
∴AF⊥BC
∵∠B=60°AB=1
∴BF=
AF=
∵BC=2
∴FC=
在RtΔAFC中AF=
FC=
∴AC=
又∵AFCE是矩形
∴EF=AC=
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
【题目】王小方开了一家服装店，专卖羽绒服，下表是去年一年各月的销售量情况：
月份 | 一 | 二 | 三 | 四 | 五 | 六 |
销售量/件 | 120 | 90 | 40 | 10 | 6 | 4 |
月份 | 七 | 八 | 九 | 十 | 十一 | 十二 |
销售量/件 | 3 | 5 | 3 | 120 | 80 | 120 |
(1)计算各季度的销售量，并用一幅合适的统计图表示；
(2)计算各季度的销售量在全年销售量中所占的百分比(精确到1%)，并用适当的统计图表示；
(3)用一幅合适的统计图表示各季度销售量的变化情况.
