题目内容
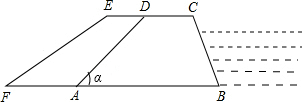
．如图，某堤坝的横截面是梯形AB—CD，背水坡AD的坡度i(即tana)为1:1.2，坝高为5m，现为了提高堤坝的防洪抗洪能力，市防汛指挥部决定加固堤坝，要求坝顶CD加宽lm，形成新的背水坡EF，其坡度为1:1.4，已知堤坝总长度为4000m．
(1)完成该工程需要多少土方?
(2)该工程由甲、乙两个工程队同时合作完成，按原计划需要20天．准备开工前接到上级通知，汛期可能提前，要求两个工程队提高工作效率，甲队工作效率提高30％，乙队工作效率提高40％，结果提前5天完成．问这两个工程队原计划每天各完成多少土方?
(1) 30000(2) 甲队原计划每天完成1000 m3土方，乙队原计划每天完成500 m 3土方
【解析】解(1)作DG⊥AB于点G，作EH⊥AB于点H．
∵CD∥AB，∴EH=DG=5 m，
∵
，∴AG=6 m，
∵
，∴FH=7 m，
∴FA=FH+GH-AG=7+1-6=2(m)．
∴S梯形ADEF=
(ED+AF)·EH= (1+2)×5=7.5(m
2)，
V=7.5×4000=30000(m 3)．
(2)设甲队原计划每天完成x m3土方，乙队原计划每天完成y m3土方．
根据题意，得
化简，得
解之，得
答：甲队原计划每天完成1000 m3土方，乙队原计划每天完成500 m 3土方．
(1)由题意可知，要求的石方数其实就是横截面为ADEF的立方体的体积．
（2）根据计划和实际分别列出两个等量关系式，根据方程组求解
小学课时特训系列答案
提高30%，乙队工作效率提高40%，结果提前5天完成．问这两个工程队原计划每天各完成多少土方？
）为1︰1.2，坝高为5米。现为了提高堤坝的防洪抗洪能力，市防汛指挥部决定加固堤坝，要求坝顶CD加宽1米，形成新的背水坡EF，其坡度为1︰1.4。已知堤坝总长度为4000米。
）为1︰1.2，坝高为5米。现为了提高堤坝的防洪抗洪能力，市防汛指挥部决定加固堤坝，要求坝顶CD加宽1米，形成新的背水坡EF，其坡度为1︰1.4。已知堤坝总长度为4000米。