题目内容
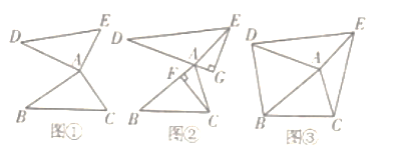
【题目】 如图，P为平行四边形ABCD的边AD上的任意一点，E，F分别为PB，PC的中点，四边形BCFE，△PDC，△PAB的面积分别为S，S1，S2，若S＝12，则S1+S2的值为（ ）
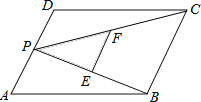
A. 12B. 14C. 16D. 18
【答案】C
【解析】
先根据平行四边形与中位线定理求出EF＝
BC，再得出△PEF∽△PBC，且相似比为1：2，求得S△PEF＝4，再求出S△PBC的面积.
解：过P作PQ∥DC交BC于点Q，由DC∥AB，得到PQ∥AB，
∴四边形PQCD与四边形APQB都为平行四边形，
∴△PDC≌△CQP，△ABP≌△QPB，
∴S△PDC＝S△CQP，S△ABP＝S△QPB，
∵EF为△PCB的中位线，
∴EF∥BC，EF＝BC，
∴△PEF∽△PBC，且相似比为1：2，
∴S△PEF：S△PBC＝
＝1：4，S四边形BCFE＝12，
∴S△PEF＝4，
∴S△PBC＝S△CQP+S△QPB＝S△PDC+S△ABP＝S1+S2＝16．
故选：C．
练习册系列答案
相关题目
