题目内容
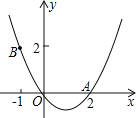
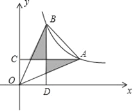
【题目】如图,点A,B为反比例函数y=![]() 在第一象限上的两点,AC⊥y轴于点C,BD⊥x轴于点D,若B点的横坐标是A点横坐标的一半,且图中阴影部分的面积为k﹣2,则k的值为( )
在第一象限上的两点,AC⊥y轴于点C,BD⊥x轴于点D,若B点的横坐标是A点横坐标的一半,且图中阴影部分的面积为k﹣2,则k的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
根据反比例函数图象上点的坐标特征,设B(t,![]() ),则AC=2CE=2t,可表示出A(2t,
),则AC=2CE=2t,可表示出A(2t,![]() ),由点B和点A的纵坐标可知BD=2OC,然后根据三角形面积公式得到关于k的方程,解此方程即可.
),由点B和点A的纵坐标可知BD=2OC,然后根据三角形面积公式得到关于k的方程,解此方程即可.
解:设B(t,![]() ),
),

∵AC⊥y轴于点C,BD⊥x轴于点D,B点的横坐标是A点横坐标的一半,
∴AC=2CE=2t,
∴A(2t,![]() ),
),
∴BD=2OC=2BE,
在△OCM和△BEM中

∴△OCM≌△BEM,
∴CM=EM=![]() ,
,
同理可证:△ODN≌△AEN,
∴EN=DN=![]() ,
,
∴阴影部分的面积=![]() .
.
解得:k=![]()
故选:B.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目