��Ŀ����
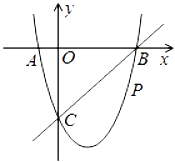
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���y��x2+bx+c��ͼ����x�ύ��A��B���㣬A����ԭ�����࣬B�������Ϊ(3��0)����y�ύ��C(0����3)�㣬��P��ֱ��BC�·�����������һ���㣮
(1)��������κ����ı���ʽ��
(2)����PO��PC�����ѡ�POC��CO���ۣ��õ��ı���POP��C����ô�Ƿ���ڵ�P��ʹ�ı���POP��CΪ���Σ������ڣ��������ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
(3)����P�˶���ʲôλ��ʱ���ı���ABPC�������������ʱP���������ı���ABPC����������
���𰸡�(1)y��x2��2x��3��(2)���ڣ�P�������Ϊ(![]() ��
��![]() )��(3)P�������Ϊ(
)��(3)P�������Ϊ(![]() ��
��![]() )���ı���ABPC����������ֵΪ
)���ı���ABPC����������ֵΪ![]() ��
��
��������
��1����B��C��������������ߵĽ���ʽ�м�����ô���ϵ����ֵ��
��2���������εĶԽ����ഹֱƽ�֣����ı���POP'CΪ���Σ���ôP�����OC�Ĵ�ֱƽ�����ϣ��ݴ˿����P��������꣬���������ߵĽ���ʽ�м������P������ꣻ
��3�����ڡ�ABC�����Ϊ��ֵ�����ı���ABPC��������ʱ����BPC��������P��y���ƽ���ߣ���ֱ��BC��Q����x����F�������ֱ��BC�Ľ���ʽ�������P��ĺ����꣬Ȼ����������ߺ�ֱ��BC�Ľ���ʽ���Q��P�������꣬���ɵõ�PQ�ij�����PQΪ�ף�B�������ľ���ֵΪ������á�BPC��������ɴ˿ɵõ������ı���ACPB�������P�������ĺ�����ϵʽ�����ݺ��������ʼ�������ı���ABPC������������Ӧ��P�����꣮
��B��C������������ã�![]() ��
��
��ã�![]() ��
��
���Զ��κ����ı���ʽΪ��y=x2��2x��3��
��2�����ڵ�P��ʹ�ı���POP'CΪ���Σ�
��P��������x��x2��2x��3����PP'��CO��E��
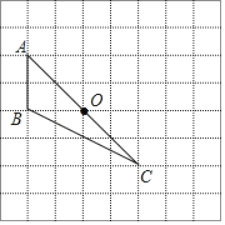
���ı���POP'C�����Σ�����PC=PO������PP'����ͼ1����PE��CO��E��
��C��0����3����
��CO=3��
�֡�OE=EC��
��OE=EC![]() ��
��
��y![]() ��
��
��x2��2x��3![]() ��
��
��ã�x1![]() ��x2
��x2![]() ���������⣬��ȥ����
���������⣬��ȥ����
��P���������![]() ����
����
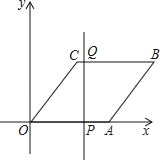
����P��y���ƽ������BC���ڵ�Q����OB���ڵ�F����ͼ2��
��P��x��x2��2x��3����
��ֱ��BC�Ľ���ʽΪ��y=kx+d����![]() ��
��
��ã�![]() ��
��
��ֱ��BC�Ľ���ʽΪy=x��3����Q�������Ϊ��x��x��3����
��0=x2��2x��3����ã�x1=��1��x2=3��
��AO=1��AB=4��S�ı���ABPC=S��ABC+S��BPQ+S��CPQ
![]() ABOC
ABOC![]() QPBF
QPBF![]() QPOF
QPOF![]()
��![]() ʱ���ı���ABPC��������
ʱ���ı���ABPC��������
��ʱP�������Ϊ![]() ���ı���ABPC����������ֵΪ
���ı���ABPC����������ֵΪ![]() ��
��


 ��У����ϵ�д�
��У����ϵ�д�