题目内容
不透明的布袋里装有红、蓝、黄三种颜色小球共40个,它们除颜色外其余都相同,其中红色球20个,蓝色球比黄色球多8个.
(1)求袋中蓝色球的个数.
(2)求摸出1个球是黄色球的概率.
(3)现再将2个黄色球放入布袋,搅匀后,求摸出1个球是黄色球的概率.
解:(1)(40-20+8)÷2=14(个).
答:袋中蓝色球的个数是14个;
(2)(20-14)÷40= .
.
故摸出1个球是黄色球的概率 .
.
(3)(20-14+2)÷(40+2)=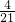 .
.
故摸出1个球是黄色球的概率是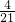 .
.
分析:(1)蓝色球的个数=(40-红色球20个+8)÷2;
(2)根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率;
(3)先求出黄色球的个数,再除以全部情况的总数,即可求解.
点评:此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)= .
.
答:袋中蓝色球的个数是14个;
(2)(20-14)÷40=
 .
.故摸出1个球是黄色球的概率
 .
.(3)(20-14+2)÷(40+2)=
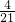 .
.故摸出1个球是黄色球的概率是
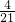 .
.分析:(1)蓝色球的个数=(40-红色球20个+8)÷2;
(2)根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率;
(3)先求出黄色球的个数,再除以全部情况的总数,即可求解.
点评:此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
 .
. 
练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 .
. .
.