题目内容
(9分) 如图,等腰梯形OABC,OC=2,AB=6,∠AOC=120°,以O为圆心,
OC为半径作⊙O,交OA于点D,动点P以每秒1个单位的速度从点A出发向点O移动,
过点P作PE∥AB,交BC于点E。设P点运动的时间为t(秒)。
(1)求OA的长;
(2)当t为何值时,PE与⊙O相切;
(3)直接写出PE与⊙O有两个公共点时t的范围,并计算,当PE与⊙O相切时,四边形PECO与⊙O重叠部分面积。
解:(1)由等腰梯形OABC,OC=2,AB=6,∠AOC=120°过O作梯形的高,得出AO=4…..3分
(2)当PE与⊙O相切时,O到PE的距离为2,得出OP=![]() ,AP=4—
,AP=4—
所以,当t=4—![]() 秒时⊙O与PE相切。…….6分
秒时⊙O与PE相切。…….6分
(3)4—![]() <t≤4,……7分,
<t≤4,……7分,
当PE与⊙O相切时,四边形PECO与⊙O重叠部分面积,即扇形OCD的面积=![]() …..9分
…..9分
解析:略

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目

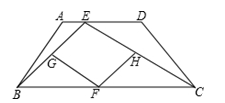
 (3)探究:在BC边上是否存在点M使得四边形PDQM是菱形?若存在,请找出点M,并求出BM的长;不存在,请说明理由.
(3)探究:在BC边上是否存在点M使得四边形PDQM是菱形?若存在,请找出点M,并求出BM的长;不存在,请说明理由.