题目内容
如图所示，△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F，若∠DEF=52°，则∠A的度数是 
76°．
解析试题分析：连接OD、OF；由圆周角定理可求得∠DOF的度数；在四边形ADOF中，∠ODA=∠OFA=90°，因此∠A和∠DOF互补，由此可求出∠A的度数．
试题解析：连接OD，OF，则∠ADO=∠AFO=90°；
由圆周角定理知，∠DOF=2∠E=104°；
∴∠A=180°-∠DOF=76°．
考点：1三角形的内切圆与内心；2.圆周角定理；3.切线的性质．
练习册系列答案
相关题目
若函数y=-2(x-1)2+(a-1)x2为二次函数，则a的取值范围为（ ）
| A．a≠0 | B．a≠1 | C．a≠2 | D．a≠3 |
”你认为正确吗？如果正确，说明理由；如果不正确，写出正确的解答过程．（2014•巴中）如图，CF是△ABC的外角∠ACM的平分线，且CF∥AB，∠ACF=50°，则∠B的度数为（ ）
| A．80° | B．40° | C．60° | D．50° |
在平面直角坐标系中，若点P（m-3,m+1）在第二象限，则m的取值范围为
| A．-1＜m＜3 | B．m＞3 | C．m＜-1 | D．m＞-1 |
的顶点均在格点上，坐标为A（1，－4），B（5，－4），C
．
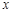轴对称的
，并写出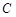点
的对称点
的坐标；
对称的
，并写出点
的坐标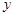
轴对称（只需写出判断结果）。