题目内容
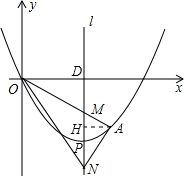
 (2012•海南)如图,顶点为P(4,-4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M、N关于点P对称,连接AN、ON,
(2012•海南)如图,顶点为P(4,-4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M、N关于点P对称,连接AN、ON,(1)求该二次函数的关系式;
(2)若点A在对称轴l右侧的二次函数图象上运动时,请解答下面问题:
①证明:∠ANM=∠ONM;
②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标;如果不能,请说明理由.
分析:(1)由二次函数的顶点坐标,设出二次函数的顶点式,再由二次函数过原点,将原点坐标代入设出的解析式中,确定出a的值,即可求出二次函数的解析式;
(2)①过A作AH垂直于直线l,直线l与x轴交于点D,由A在二次函数图象上,设A横坐标为m,将x=m代入二次函数解析式,表示出纵坐标,确定出A的坐标,再由O的坐标,表示出直线AO的解析式,进而表示出M,N及H的坐标,得出OD,ND,HA,及NH,在直角三角形OND中,利用锐角三角函数定义表示出tan∠ONM,在直角三角形ANH中,利用锐角三角函数定义表示出tan∠ANM,化简后得到tan∠ONM=tan∠ANM,可得出∠ONM=∠ANM,得证;
②△ANO能为直角三角形,理由为:分三种情况考虑:若∠ONA为直角,由①得到∠ANM=∠ONM=45°,可得出三角形AHN为等腰直角三角形,得到AH=HN,将表示出的AH及HN代入,得到关于m的方程,求出方程的解得到m的值为0或4±
,进而得到此时A与P重合,不合题意,故∠ONA不能为直角;若∠AON为直角,利用勾股定理得到OA2+ON2=AN2,由A的坐标,利用勾股定理表示出OA2,由OD及DN,利用勾股定理表示出ON2,由AH及HN,利用勾股定理表示出AN2,代入OA2+ON2=AN2,得到关于m的方程,求出方程的解得到m的值为4±4
或0,然后判断∠AON是否为直角;若∠NAO为直角,则有△AMN∽△DMO∽△DON,由相似得比例,将各自的值代入得到关于m的方程,求出方程的解得到m的值为4,此时A与P重合,故∠NAO不能为直角,综上,点A在对称轴l右侧的二次函数图象上运动时,△ANO不能为直角三角形.
(2)①过A作AH垂直于直线l,直线l与x轴交于点D,由A在二次函数图象上,设A横坐标为m,将x=m代入二次函数解析式,表示出纵坐标,确定出A的坐标,再由O的坐标,表示出直线AO的解析式,进而表示出M,N及H的坐标,得出OD,ND,HA,及NH,在直角三角形OND中,利用锐角三角函数定义表示出tan∠ONM,在直角三角形ANH中,利用锐角三角函数定义表示出tan∠ANM,化简后得到tan∠ONM=tan∠ANM,可得出∠ONM=∠ANM,得证;
②△ANO能为直角三角形,理由为:分三种情况考虑:若∠ONA为直角,由①得到∠ANM=∠ONM=45°,可得出三角形AHN为等腰直角三角形,得到AH=HN,将表示出的AH及HN代入,得到关于m的方程,求出方程的解得到m的值为0或4±
| 2 |
| 2 |
解答:解:(1)∵二次函数的顶点坐标为(4,-4),
∴设二次函数的解析式为y=a(x-4)2-4,
又二次函数过(0,0),
∴0=a(0-4)2-4,解得:a=
,
∴二次函数解析式为y=
(x-4)2-4=
x2-2x;
(2)①证明:过A作AH⊥l于H,l与x轴交于点D,如图所示:
设A(m,
m2-2m),又O(0,0),
∴直线AO的解析式为y=
x=(
m-2)x,
则M(4,m-8),N(4,-m),H(4,
m2-2m),
∴OD=4,ND=m,HA=m-4,NH=ND-HD=
m2-m,
在Rt△OND中,tan∠ONM=
=
,
在Rt△ANH中,tan∠ANM=
=
=
=
,
∴tan∠ONM=tan∠ANM,
则∠ANM=∠ONM;
②△ANO能为直角三角形,理由如下:
分三种情况考虑:
(i)若∠ONA为直角,由①得:∠ANM=∠ONM=45°,
∴△AHN为等腰直角三角形,
∴HA=NH,即m-4=
m2-m,
整理得:m2-8m+16=0,即(m-4)2=0,
解得:m=4,
此时点A与点P重合,故不存在A点使△ONA为直角三角形;
(ii)若∠AON为直角,根据勾股定理得:OA2+ON2=AN2,
∵OA2=m2+(
m2-2m)2,ON2=42+m2,AN2=(m-4)2+(
m2-2m+m)2,
∴m2+(
m2-2m)2+42+m2=(m-4)2+(
m2-2m+m)2,
整理得:m(m2-8m-16)=0,
解得:m=0或m=4+4
或4-4
(舍去),
当m=0时,A点与原点重合,故∠AON不能为直角,
当m=4+4
,即A(4+4
,4)时,N为第四象限点,成立,故∠AON能为直角;
(iii)若∠NAO为直角,可得∠NAM=∠ODM=90°,且∠AMN=∠DMO,
∴△AMN∽△DMO,
又∠MAN=∠ODN=90°,且∠ANM=∠OND,
∴△AMN∽△DON,
∴△AMN∽△DMO∽△DON,
∴
=
,即
=
,
整理得:(m-4)2=0,
解得:m=4,
此时A与P重合,故∠NAO不能为直角,
综上,点A在对称轴l右侧的二次函数图象上运动时,△ANO能为直角三角形,当m=4+4
,即A(4+4
,4)时,N为第四象限点,成立,故∠AON能为直角.
∴设二次函数的解析式为y=a(x-4)2-4,
又二次函数过(0,0),
∴0=a(0-4)2-4,解得:a=
| 1 |
| 4 |
∴二次函数解析式为y=
| 1 |
| 4 |
| 1 |
| 4 |
(2)①证明:过A作AH⊥l于H,l与x轴交于点D,如图所示:

设A(m,
| 1 |
| 4 |
∴直线AO的解析式为y=
| ||
| m |
| 1 |
| 4 |
则M(4,m-8),N(4,-m),H(4,
| 1 |
| 4 |
∴OD=4,ND=m,HA=m-4,NH=ND-HD=
| 1 |
| 4 |
在Rt△OND中,tan∠ONM=
| OD |
| DN |
| 4 |
| m |
在Rt△ANH中,tan∠ANM=
| HA |
| HN |
| m-4 | ||
|
| 4(m-4) |
| m(m-4) |
| 4 |
| m |
∴tan∠ONM=tan∠ANM,
则∠ANM=∠ONM;
②△ANO能为直角三角形,理由如下:
分三种情况考虑:
(i)若∠ONA为直角,由①得:∠ANM=∠ONM=45°,
∴△AHN为等腰直角三角形,
∴HA=NH,即m-4=
| 1 |
| 4 |
整理得:m2-8m+16=0,即(m-4)2=0,
解得:m=4,
此时点A与点P重合,故不存在A点使△ONA为直角三角形;
(ii)若∠AON为直角,根据勾股定理得:OA2+ON2=AN2,
∵OA2=m2+(
| 1 |
| 4 |
| 1 |
| 4 |
∴m2+(
| 1 |
| 4 |
| 1 |
| 4 |
整理得:m(m2-8m-16)=0,
解得:m=0或m=4+4
| 2 |
| 2 |
当m=0时,A点与原点重合,故∠AON不能为直角,
当m=4+4
| 2 |
| 2 |
(iii)若∠NAO为直角,可得∠NAM=∠ODM=90°,且∠AMN=∠DMO,
∴△AMN∽△DMO,
又∠MAN=∠ODN=90°,且∠ANM=∠OND,
∴△AMN∽△DON,
∴△AMN∽△DMO∽△DON,
∴
| MD |
| OD |
| OD |
| ND |
| 8-m |
| 4 |
| 4 |
| m |
整理得:(m-4)2=0,
解得:m=4,
此时A与P重合,故∠NAO不能为直角,
综上,点A在对称轴l右侧的二次函数图象上运动时,△ANO能为直角三角形,当m=4+4
| 2 |
| 2 |
点评:此题考查了利用待定系数法求二次函数解析式,两点坐标确定一次函数解析式,锐角三角函数定义,等腰直角三角形的判定与性质,勾股定理,以及相似三角形的判定与性质,本题(2)中的第②小问利用的是反证法,先假设结论成立,利用逻辑推理的方法得出与已知条件,定理,公理矛盾,可得出假设错误,原结论不成立.

练习册系列答案
相关题目
 (2012•海南)如图,在△ABC中,∠B与∠C的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.若AB=5,AC=4,则△ADE的周长是
(2012•海南)如图,在△ABC中,∠B与∠C的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.若AB=5,AC=4,则△ADE的周长是 (2012•海南)如图,正比例函数y=k1x与反比例函数y=
(2012•海南)如图,正比例函数y=k1x与反比例函数y= (2012•海南)如图,点A、B、O是正方形网格上的三个格点,⊙O的半径是OA,点P是优弧
(2012•海南)如图,点A、B、O是正方形网格上的三个格点,⊙O的半径是OA,点P是优弧
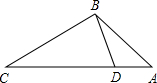 (2012•海南)如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )
(2012•海南)如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )