题目内容
矩形ABCD中,对角线AC=4,∠ACB=30°,以直线AB为轴旋转一周得到圆柱的表面积是________.
(24+8 )π
)π
分析:易得矩形两条边长,那么圆柱的表面积=侧面积+两个底面积=底面周长×高+2π半径2.
解答: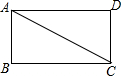 解:∵矩形ABCD中,对角线AC=4,∠ACB=30°,
解:∵矩形ABCD中,对角线AC=4,∠ACB=30°,
∴AB=2,AD=2 ,
,
∴以直线AB为轴旋转一周得到圆柱的底面周长为:2×2 ×π=4
×π=4 π,
π,
所以以直线AB为轴旋转一周得到圆柱的表面积为:
2×4 π+π×(2
π+π×(2 )2×2=(24+8
)2×2=(24+8 )π.
)π.
点评:本题的关键是选利用解直角三角形求出矩形的长和宽,然后再求表面积,注意表面积=侧面积+两个底面积.
 )π
)π分析:易得矩形两条边长,那么圆柱的表面积=侧面积+两个底面积=底面周长×高+2π半径2.
解答:
 解:∵矩形ABCD中,对角线AC=4,∠ACB=30°,
解:∵矩形ABCD中,对角线AC=4,∠ACB=30°,∴AB=2,AD=2
 ,
,∴以直线AB为轴旋转一周得到圆柱的底面周长为:2×2
 ×π=4
×π=4 π,
π,所以以直线AB为轴旋转一周得到圆柱的表面积为:
2×4
 π+π×(2
π+π×(2 )2×2=(24+8
)2×2=(24+8 )π.
)π.点评:本题的关键是选利用解直角三角形求出矩形的长和宽,然后再求表面积,注意表面积=侧面积+两个底面积.

练习册系列答案
相关题目
 =∠DCE.
=∠DCE. 如图,矩形ABCD中,AB=8,BC=9,⊙E和⊙F相外切,且它们分别与矩形的一对对角的两边相切,则圆心距EF=
如图,矩形ABCD中,AB=8,BC=9,⊙E和⊙F相外切,且它们分别与矩形的一对对角的两边相切,则圆心距EF= ,AE=7,求⊙O的直径。
,AE=7,求⊙O的直径。
 ,AE=7,求⊙O的直径.
,AE=7,求⊙O的直径.
 ,AE=7,求⊙O的直径.
,AE=7,求⊙O的直径.