题目内容
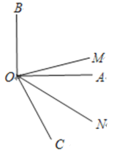
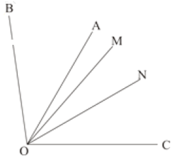
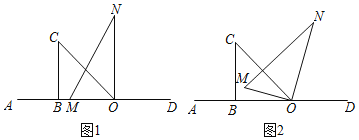
【题目】将一副直角三角板按如图1摆放在直线AD上![]() 直角三角板OBC和直角三角板MON,
直角三角板OBC和直角三角板MON,![]() ,
,![]() ,
,![]() ,
,![]() ,保持三角板OBC不动,将三角板MON绕点O以每秒
,保持三角板OBC不动,将三角板MON绕点O以每秒![]() 的速度顺时针方向旋转t秒
的速度顺时针方向旋转t秒![]()
![]() 如图2,
如图2,![]() ______度
______度![]() 用含t的式子表示
用含t的式子表示![]() ;
;
![]() 在旋转的过程中,是否存在t的值,使
在旋转的过程中,是否存在t的值,使![]() ?若存在,请求出t的值;若不存在,请说明理由.
?若存在,请求出t的值;若不存在,请说明理由.
![]() 直线AD的位置不变,若在三角板MON开始顺时针旋转的同时,另一个三角板OBC也绕点O以每秒
直线AD的位置不变,若在三角板MON开始顺时针旋转的同时,另一个三角板OBC也绕点O以每秒![]() 的速度顺时针旋转.
的速度顺时针旋转.
![]() 当
当![]() ______秒时,
______秒时,![]() ;
;
![]() 请直接写出在旋转过程中,
请直接写出在旋转过程中,![]() 与
与![]() 的数量关系
的数量关系![]() 关系式中不能含
关系式中不能含![]() .
.
【答案】(1)![]() (2)
(2)![]() (3)①5或10,②3∠NOD+4∠BOM=270°.
(3)①5或10,②3∠NOD+4∠BOM=270°.
【解析】
(1)把旋转前∠NOD的大小减去旋转的度数就是旋转后的∠NOD的大小.
(2)相对MO与CO的位置有两种情况,所以要分类讨论,然后根据∠NOD=4∠COM建立关于t的方程即可.
(3)①其实是一个追赶问题,分MO没有追上CO与MO超过CO两种情况,然后分别列方程即可.
②分别用t的代数式表示∠NOD和∠BOM,然后消去t即可得出它们的关系.
(1)∠NOD一开始为90°,然后每秒减少8°,因此∠NOD=90﹣8t.
故答案为:90﹣8t.
(2)当MO在∠BOC内部时,即t![]() 时,根据题意得:
时,根据题意得:
90﹣8t=4(45﹣8t)
解得:t![]() ;
;
当MO在∠BOC外部时,即t![]() 时,根据题意得:
时,根据题意得:
90﹣8t=4(8t﹣45)
解得:t![]() .
.
综上所述:t![]() 或t
或t![]() .
.
(3)①当MO在∠BOC内部时,即t![]() 时,根据题意得:
时,根据题意得:
8t﹣2t=30
解得:t=5;
当MO在∠BOC外部时,即t![]() 时,根据题意得:
时,根据题意得:
8t﹣2t=60
解得:t=10.
故答案为:5或10.
②∵∠NOD=90﹣8t,∠BOM=6t,∴3∠NOD+4∠BOM=3(90﹣8t)+4×6t=270°.
即3∠NOD+4∠BOM=270°.