题目内容
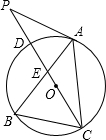 如图,点A、B、C分别是⊙O上的点,CD是⊙O的直径,P是CD延长线上的一点,AP=AC.
如图,点A、B、C分别是⊙O上的点,CD是⊙O的直径,P是CD延长线上的一点,AP=AC.
(1)若∠B=60°.求证:AP是⊙O的切线;
(2)若点B是弧CD的中点,AB交CD于点E,CD=4,求BE•AB的值.
(1)证明: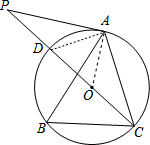 连接AD,OA,
连接AD,OA,
∵∠ADC=∠B,∠B=60°,
∴∠ADC=60°,
∵CD是直径,
∴∠DAC=90°,
∴∠ACO=180°-90°-60°=30°,
∵AP=AC,OA=OC,
∴∠OAC=∠ACD=30°,∠P=∠ACD=30°,
∴∠OAP=180°-30°-30°-30°=90°,
即OA⊥AP,
∵OA为半径,
∴AP是⊙O切线.
(2)解: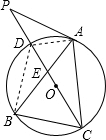 连接AD,BD,
连接AD,BD,
∵CD是直径,
∴∠DBC=90°,
∵CD=4,
∴BD=BC=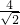 =2
=2 ,
,
∵B为弧CD中点,
∴BD=BC,
∴∠BDC=∠BCD=45°,
∴∠DAB=∠DCB=45°,
即∠BDE=∠DAB,
∵∠DBE=∠DBA,
∴△DBE∽△ABD,
∴ =
= ,
,
∴BE•AB=BD•BD=2 ×2
×2 =8.
=8.
分析:(1)求出∠ADC的度数,求出∠P、∠ACO、∠OAC度数,求出∠OAP=90°,根据切线判定推出即可;
(2)求出BD长,求出△DBE和△ABD相似,得出比例式,代入即可求出答案.
点评:本题考查了圆周角定理,勾股定理,等腰三角形性质和判定,相似三角形的性质和判定,切线的判定的应用,主要考查学生综合运用性质进行推理和计算的能力.
 连接AD,OA,
连接AD,OA,∵∠ADC=∠B,∠B=60°,
∴∠ADC=60°,
∵CD是直径,
∴∠DAC=90°,
∴∠ACO=180°-90°-60°=30°,
∵AP=AC,OA=OC,
∴∠OAC=∠ACD=30°,∠P=∠ACD=30°,
∴∠OAP=180°-30°-30°-30°=90°,
即OA⊥AP,
∵OA为半径,
∴AP是⊙O切线.
(2)解:
 连接AD,BD,
连接AD,BD,∵CD是直径,
∴∠DBC=90°,
∵CD=4,
∴BD=BC=
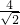 =2
=2 ,
,∵B为弧CD中点,
∴BD=BC,
∴∠BDC=∠BCD=45°,
∴∠DAB=∠DCB=45°,
即∠BDE=∠DAB,
∵∠DBE=∠DBA,
∴△DBE∽△ABD,
∴
 =
= ,
,∴BE•AB=BD•BD=2
 ×2
×2 =8.
=8.分析:(1)求出∠ADC的度数,求出∠P、∠ACO、∠OAC度数,求出∠OAP=90°,根据切线判定推出即可;
(2)求出BD长,求出△DBE和△ABD相似,得出比例式,代入即可求出答案.
点评:本题考查了圆周角定理,勾股定理,等腰三角形性质和判定,相似三角形的性质和判定,切线的判定的应用,主要考查学生综合运用性质进行推理和计算的能力.

练习册系列答案
相关题目
 如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )
如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )| A、EF与AD互相平分 | ||
B、EF=
| ||
| C、AD平分∠BAC | ||
| D、△DEF∽△ACB |
 如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )
如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )| A、AD平分∠BAC | ||
B、EF=
| ||
| C、EF与AD互相平分 | ||
| D、△DFE是△ABC的位似图形 |
 5、如图,点D、E、F分别是△ABC的边AB、BC、AC的中点,连接DE、EF,要使四边形ADEF为正方形,还需增加条件:
5、如图,点D、E、F分别是△ABC的边AB、BC、AC的中点,连接DE、EF,要使四边形ADEF为正方形,还需增加条件: 如图,点D,E,F分别是△ABC的三边AB,AC,BC上的中点,如果△ABC的面积是18cm2,则△DBF的面积是
如图,点D,E,F分别是△ABC的三边AB,AC,BC上的中点,如果△ABC的面积是18cm2,则△DBF的面积是 如图,点D、E、F分别是△ABC三边AB、BC、AC的中点,则△DEF的周长是△ABC周长的( )
如图,点D、E、F分别是△ABC三边AB、BC、AC的中点,则△DEF的周长是△ABC周长的( )