题目内容
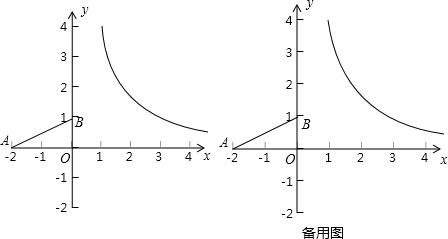
如图,点A(-2,0),点B(0,1),双曲线y=| 4 | x |
(1)将线段AB绕点O顺时针旋转90°,得到线段A1B1,写出A1、B1的坐标;
(2)将线段A1B1平移,对应点A2,B2落在双曲线上,求出点A2,B2的坐标;
(3)将双曲线绕点M旋转90°,旋转后的双曲线是否能同时经过A、B两点?若能,求出点M的坐标;若不能,请说明理由.
分析:(1)由题意旋转后很容易得;
(2)设A2,根据平移的性质得B2,求得a值,从而求得A2(1,4),B2(2,2).②对应点的连线经过旋转中心,求得点D.用同样方法求出直线A2M的解析式,求得点M.
(3)由(1)(2)小题知AB⊥A2B2,所以可绕某一点将AB旋转90度与A2B2重合,又由BM=MB2,所以得△BMB2是等腰直角三角形.以BB2为一边,M为中心,构造正方形,易知点M.
(2)设A2,根据平移的性质得B2,求得a值,从而求得A2(1,4),B2(2,2).②对应点的连线经过旋转中心,求得点D.用同样方法求出直线A2M的解析式,求得点M.
(3)由(1)(2)小题知AB⊥A2B2,所以可绕某一点将AB旋转90度与A2B2重合,又由BM=MB2,所以得△BMB2是等腰直角三角形.以BB2为一边,M为中心,构造正方形,易知点M.
解答:解:(1)(0,2)(1,0);
(2)∵A2在双曲线y=
(x>0)上,
设A2(a,
),且a>0,
根据平移的性质得B2(a+1,
-2),
∵B2在双曲线y=
(x>0)上,
∴(a+1)(
-2)=4,
解得a1=1,a2=-2,
经检验是方程的根,
∵a>0,
∴a=1,
∴A2(1,4)B2(2,2),
(3)由(1)(2)小题知AB⊥A2B2,所以可绕某一点将AB旋转90度与A2B2重合,(1分
又∵若将双曲线绕某一点旋转90°,使之同时经过A、B两点,等同于将AB绕某一点旋转90度,使A、B两点同时落在双曲线上,
①若将AB绕点M旋转顺时针90度,
A与A2,B与B2对应,如图1
连接BB2接,点M在BB2的对称轴上,
∴BM=MB2,
∵旋转角∠BMB2=90°,
∴△BMB2是等腰直角三角形,
以BB2为一边,M为中心,构造正方形,易知M(
,
).
②将AB绕点M旋转逆时针90度,
∵对应点的连线经过旋转中心,
∴作AB2,BA2若的对称轴,交于点M,
用相似求出点D(
,0),直线BD的解析式y=-2x+1,
用同样方法求出直线A2M的解析式y=-
x+
,
∴M(-1,3),
综上M(-1,3)或(
,
); (两种情况,分别用两种方法解仅供参考);

(2)∵A2在双曲线y=
| 4 |
| x |
设A2(a,
| 4 |
| a |
根据平移的性质得B2(a+1,
| 4 |
| a |
∵B2在双曲线y=
| 4 |
| x |
∴(a+1)(
| 4 |
| a |
解得a1=1,a2=-2,
经检验是方程的根,
∵a>0,
∴a=1,
∴A2(1,4)B2(2,2),
(3)由(1)(2)小题知AB⊥A2B2,所以可绕某一点将AB旋转90度与A2B2重合,(1分
又∵若将双曲线绕某一点旋转90°,使之同时经过A、B两点,等同于将AB绕某一点旋转90度,使A、B两点同时落在双曲线上,
①若将AB绕点M旋转顺时针90度,
A与A2,B与B2对应,如图1
连接BB2接,点M在BB2的对称轴上,
∴BM=MB2,
∵旋转角∠BMB2=90°,
∴△BMB2是等腰直角三角形,
以BB2为一边,M为中心,构造正方形,易知M(
| 3 |
| 2 |
| 1 |
| 2 |
②将AB绕点M旋转逆时针90度,
∵对应点的连线经过旋转中心,
∴作AB2,BA2若的对称轴,交于点M,
用相似求出点D(
| 1 |
| 2 |
用同样方法求出直线A2M的解析式y=-
| 1 |
| 2 |
| 5 |
| 2 |
∴M(-1,3),
综上M(-1,3)或(
| 3 |
| 2 |
| 1 |
| 2 |

点评:本题考查了反比例函数的综合应用,(1)通过旋转来确定坐标;(2)设A2,根据平移的性质得B2,求得a值,从而求得A2(1,4),B2(2,2).②对应点的连线经过旋转中心,求得点D.进而求得点M.(3)由(1)(2)小题知AB⊥A2B2,所以可绕某一点将AB旋转90度与A2B2重合,又由BM=MB2,所以得△BMB2是等腰直角三角形.以BB2为一边,M为中心,构造正方形,易知点M.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
 如图,点A的坐标为(2
如图,点A的坐标为(2| 2 |
| A、(0,0) | ||||||||
B、(
| ||||||||
| C、(1,1) | ||||||||
D、(
|

 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°.
 12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是
12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是