Question

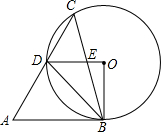（2012•温州模拟）如图，在锐角△ABC中，∠A=60°，∠ACB=45°，以BC为弦作⊙O，交AC于点D，OD与BC交于点E，若AB与⊙O相切，则下列结论：
①∠BOD=90°；②DO∥AB；③CD=AD；④△BDE∽△BCD；⑤

BE

DE

=

2

正确的有（　　）

A．①②

B．①④⑤

C．①②④⑤

D．①②③④⑤

Answer 1

分析：根据圆周角定理即可求出∠DOB=90°，判断①即可；根据切线性质得出∠OBA=90°，根据平行线的判定即可判断②；用反证法推出CE=BE，根据垂径定理得出OD⊥BC，根据三角形的内角和定理即可判定假设不成立，即可判断③；求出∠ODB的度数得出∠ODB=∠C，再加上∠CBD=∠CBD，根据相似三角形的判定即可推出④，过E作EM⊥BD于M，设DM=EM=a，由勾股定理求出DE=

2

a，BE=2EM=2a，代入求出即可．

解答：解：∵∠ACB=45°，
∴由圆周角定理得：∠BOD=2∠ACB=90°，∴①正确；
∵AB切⊙O于B，
∴∠ABO=90°，
∴∠DOB+∠ABO=180°，
∴DO∥AB，∴②正确；
假如CD=AD，因为DO∥AB，
所以CE=BE，
根据垂径定理得：OD⊥BC，
则∠OEB=90°，
∵已证出∠DOB=90°，
∴此时△OEB不存在，∴③错误；
∵∠DOB=90°，OD=OB，
∴∠ODB=∠OBD=45°=∠ACB，
即∠ODB=∠C，
∵∠DBE=∠CBD，
∴△BDE∽△BCD，∴④正确；
过E作EM⊥BD于M，
则∠EMD=90°，
∵∠ODB=45°，
∴∠DEM=45°=∠EDM，
∴DM=EM，
设DM=EM=a，
则由勾股定理得：DE=

2

a，
∵∠ABC=180°-∠C-∠A=75°，
又∵∠OBA=90°，∠OBD=45°，
∴∠OBC=15°，
∴∠EBM=30°，
在Rt△EMB中BE=2EM=2a，
∴

BE

DE

=

2a

2 a

=

2

，∴⑤正确；
故选C．

点评：本题考查了圆周角定理，切线的性质，三角形的内角和定理，含30度角的直角三角形，等腰三角形的性质和判定，相似三角形的判定等知识点，主要考查学生综合运用性质进行推理的能力，题目比较好，但是一道难度偏大的题目．