Question

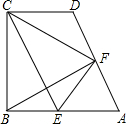（2013•杭州一模）在直角梯形ABCD中，AB∥CD，∠ABC=90°，∠A=60°，AB=2CD，E，F分别为AB，AD的中点，连结EF，EC，BF，CF．
（1）求证△CBE≌△CFE；
（2）若CD=a，求四边形BCFE的面积．

Answer 1

分析：连接DE，求出CD=BE，得出矩形BEDC，推出∠DEB=90°，根据直角三角形斜边上中线性质得出FE=AF，得出等边三角形EFA，求出EF=AE=BE，∠EFA=60°，求出∠DFC=30°，求出∠CFE=90°，根据HL证出直角三角形全等即可；
（2）根据勾股定理求出DE，BC，求出△CBE面积，即可求出答案．

解答：（1）证明：连接DE，
∵E为AB的中点，
∴AB=2AE=2BE，
∵AB=2DC，
∴CD=BE，
∵CD∥AB，∠CBA=90°，
∴四边形CBED是矩形，
∵F为AD中点，∠DEA=90°，
∴EF=AF，
∵∠A=60°，
∴△AEF是正三角形，
∴AE=EF=AF，∠EFA=60°，
∵AE=BE，DF=AF
∴BE=EF=AF，CD=DF，
∴∠CFE=90°=∠CBE，
∵CD∥AB，
∴∠CDF=180°-∠A=120°，
∴∠DFC=30°，
∴∠CFE=90°=∠CBE，
∵在Rt△CBE和Rt△CFE中

CE=CE BE=EF

∴Rt△CBE≌Rt△CFE（HL）；

（2）解：∵CD=a，
∴AE=BE=a，
∵∠A=60°，
∴BC=DE=

3

a，
∴S△BCE=

3

2

a2，
∴S_{四边形BCFE}=2S_△BCE=

3

a²．

点评：本题考查了梯形性质，矩形的性质和判定，等边三角形的性质和判定，平行线的性质，三角形的内角和定理，等腰三角形的性质，勾股定理等知识点的应用，主要考查学生综合运用性质进行推理的能力，题目综合性比较强，难度偏大．