题目内容
20、已知A为⊙O上一点,B为⊙A与OA的交点,⊙A与⊙O的半径分别为r、R,且r<R.
(Ⅰ)如图,过点B作⊙A的切线与⊙O交于M、N两点.求证:AM•AN=2Rr;
(Ⅱ)如图,若⊙A与⊙O的交点为E、F,C是弧EBF上任意一点,过点C作⊙A的切线与⊙O交于P、Q两点,试问AP•AQ=2Rr是否成立,并证明你的结论.
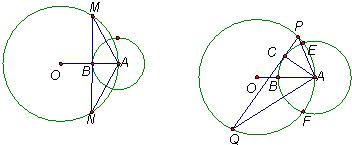
(Ⅰ)如图,过点B作⊙A的切线与⊙O交于M、N两点.求证:AM•AN=2Rr;
(Ⅱ)如图,若⊙A与⊙O的交点为E、F,C是弧EBF上任意一点,过点C作⊙A的切线与⊙O交于P、Q两点,试问AP•AQ=2Rr是否成立,并证明你的结论.

分析:(Ⅰ)欲证AM•AN=2Rr,即证AM•AM=AD•AB,可通过证△ABM∽△AMD得出;
(Ⅱ)欲证AP•AQ=2Rr,即证AP•AQ=AD•AC,可通过证△AQC∽△APD得出.
(Ⅱ)欲证AP•AQ=2Rr,即证AP•AQ=AD•AC,可通过证△AQC∽△APD得出.
解答: 解:(Ⅰ)延长AO交⊙O于D,连接MD,
解:(Ⅰ)延长AO交⊙O于D,连接MD,
∵过点B作⊙A的切线与⊙O交于M、N两点
∴OA⊥MN,AM=AN
∵AD是⊙O的直径
∴∠AMD=∠ABM=90°
∵∠MAD=∠MAD
∴△ABM∽△AMD
∴AM:AB=AD:AM
∴AM:AB=AD:AN
∴AM•AN=2Rr;
(Ⅱ)延长AO交⊙O于D,连接PD,
∵过点C作⊙A的切线与⊙O交于P、Q两点,
∴CA⊥PQ
∵AD是⊙O的直径
∴∠APD=∠ACQ=90°
∵∠Q=∠D
∴△AQC∽△APD
∴AC:AQ=AD:AP
∴AP•AQ=2Rr.
 解:(Ⅰ)延长AO交⊙O于D,连接MD,
解:(Ⅰ)延长AO交⊙O于D,连接MD,∵过点B作⊙A的切线与⊙O交于M、N两点
∴OA⊥MN,AM=AN
∵AD是⊙O的直径
∴∠AMD=∠ABM=90°
∵∠MAD=∠MAD
∴△ABM∽△AMD
∴AM:AB=AD:AM
∴AM:AB=AD:AN
∴AM•AN=2Rr;
(Ⅱ)延长AO交⊙O于D,连接PD,
∵过点C作⊙A的切线与⊙O交于P、Q两点,
∴CA⊥PQ
∵AD是⊙O的直径
∴∠APD=∠ACQ=90°
∵∠Q=∠D
∴△AQC∽△APD
∴AC:AQ=AD:AP
∴AP•AQ=2Rr.
点评:考查圆与圆的位置关系中乘积的形式,乘积的形式通常可以转化为比例的形式,通过证明三角形相似得出.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数.
如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数. 16、如图,已知D为BC上一点,∠B=∠1,∠BAC=78°,则∠2=
16、如图,已知D为BC上一点,∠B=∠1,∠BAC=78°,则∠2= 25、如图,已知O为⊙O′上一点,⊙O和⊙O/相交于A,B,CD是⊙O的直径,交AB于F,DC的延长线交⊙O′于E,且CF=4,OF=2,则CE的长为( )
25、如图,已知O为⊙O′上一点,⊙O和⊙O/相交于A,B,CD是⊙O的直径,交AB于F,DC的延长线交⊙O′于E,且CF=4,OF=2,则CE的长为( )