题目内容
如图,在直角梯形AOCB中,AB∥OC,∠AOC=90°,AB=1,AO=2,OC=3,以O为原点,OC、OA所在直线为轴建立坐标系.抛物线顶点为A,且经过点C.点P在线段AO上由A向点O运动,点O在线段OC上由C向点O运动,QD⊥OC交BC于点D,OD所在直线与抛物线在第一象限交于点E.
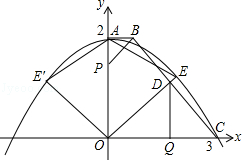
(1)求抛物线的解析式;
(2)点E′是E关于y轴的对称点,点Q运动到何处时,四边形OEAE′是菱形?
(3)点P、Q分别以每秒2个单位和3个单位的速度同时出发,运动的时间为t秒,当t为何值时,PB∥OD?

(1)求抛物线的解析式;
(2)点E′是E关于y轴的对称点,点Q运动到何处时,四边形OEAE′是菱形?
(3)点P、Q分别以每秒2个单位和3个单位的速度同时出发,运动的时间为t秒,当t为何值时,PB∥OD?
解:(1)∵A(0,2)为抛物线的顶点,∴设y=ax2+2。
∵点C(3,0),在抛物线上,∴9a+2=0,解得: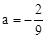 。
。
∴抛物线的解析式为; 。
。
(2)若要四边形OEAE′是菱形,则只要AO与EE′互相垂直平分,
∴EE′经过AO的中点,∴点E纵坐标为1,代入抛物线解析式得: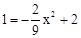 ,
,
解得: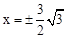 。
。
∵点E在第一象限,∴点E为(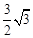 ,1)。
,1)。
设直线BC的解析式为y=kx+b,
把B(1,2),C(3,0),代入得: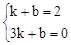 ,解得
,解得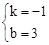 。
。
∴BC的解析式为: 。
。
设直线EO的解析式为y=ax,将E点代入,可得出EO的解析式为: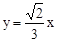 。
。
由 ,得:
,得: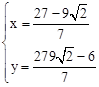 ,
,
∴直线EO和直线BC的交点坐标为:(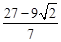 ,
,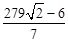 )。
)。
∴Q点坐标为:(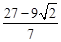 ,0)。
,0)。
∴当Q点坐标为(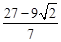 ,0)时,四边形OEAE′是菱形。
,0)时,四边形OEAE′是菱形。
(3)设t为m秒时,PB∥DO,又QD∥y轴,则有∠APB=∠AOE=∠ODQ,
又∵∠BAP=∠DQO,则有△APB∽△QDO。
∴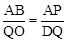 。
。
由题意得:AB=1,AP=2m,QO=3﹣3m,
又∵点D在直线y=﹣x+3上,∴DQ=3m。
∴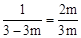 ,解得:
,解得: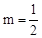 。
。
经检验: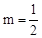 是原分式方程的解。
是原分式方程的解。
∴当t=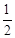 秒时,PB∥OD。
秒时,PB∥OD。
∵点C(3,0),在抛物线上,∴9a+2=0,解得:
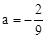 。
。∴抛物线的解析式为;
 。
。(2)若要四边形OEAE′是菱形,则只要AO与EE′互相垂直平分,
∴EE′经过AO的中点,∴点E纵坐标为1,代入抛物线解析式得:
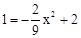 ,
,解得:
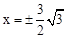 。
。∵点E在第一象限,∴点E为(
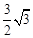 ,1)。
,1)。设直线BC的解析式为y=kx+b,
把B(1,2),C(3,0),代入得:
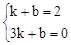 ,解得
,解得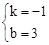 。
。∴BC的解析式为:
 。
。设直线EO的解析式为y=ax,将E点代入,可得出EO的解析式为:
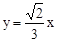 。
。由
 ,得:
,得: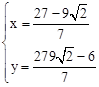 ,
,∴直线EO和直线BC的交点坐标为:(
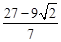 ,
,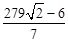 )。
)。∴Q点坐标为:(
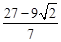 ,0)。
,0)。∴当Q点坐标为(
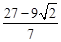 ,0)时,四边形OEAE′是菱形。
,0)时,四边形OEAE′是菱形。(3)设t为m秒时,PB∥DO,又QD∥y轴,则有∠APB=∠AOE=∠ODQ,
又∵∠BAP=∠DQO,则有△APB∽△QDO。
∴
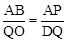 。
。由题意得:AB=1,AP=2m,QO=3﹣3m,
又∵点D在直线y=﹣x+3上,∴DQ=3m。
∴
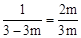 ,解得:
,解得: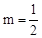 。
。经检验:
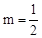 是原分式方程的解。
是原分式方程的解。∴当t=
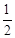 秒时,PB∥OD。
秒时,PB∥OD。(1)根据顶点式将A,C代入解析式求出a的值,进而得出二次函数解析式。
(2)利用菱形的判定得出AO与EE′互相垂直平分,利用E点纵坐标得出x的值,进而得出BC,EO直线解析式,再利用两直线交点坐标求法得出Q点坐标,即可得出答案。
(3)首先得出△APB∽△QDO,进而得出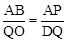 ,求出m的值,进而得出答案。
,求出m的值,进而得出答案。
(2)利用菱形的判定得出AO与EE′互相垂直平分,利用E点纵坐标得出x的值,进而得出BC,EO直线解析式,再利用两直线交点坐标求法得出Q点坐标,即可得出答案。
(3)首先得出△APB∽△QDO,进而得出
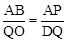 ,求出m的值,进而得出答案。
,求出m的值,进而得出答案。
练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 与y轴的交点为(0,﹣3),则下列说法不正确的是【 】
与y轴的交点为(0,﹣3),则下列说法不正确的是【 】
 )在直线MG上。问:当m为何值时,在抛物线C3上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形?
)在直线MG上。问:当m为何值时,在抛物线C3上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形? 的图象过C点.
的图象过C点.
 经过B,H, D三点,求抛物线解析式;
经过B,H, D三点,求抛物线解析式;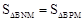 如果存在,求出点P的坐标;如果不存在,请说明理由.
如果存在,求出点P的坐标;如果不存在,请说明理由.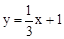 与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.
与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.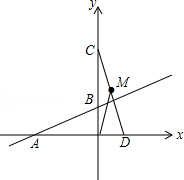
 个单位后得到的抛物线的解析式.
个单位后得到的抛物线的解析式.
 、二次函数
、二次函数 和反比例函数
和反比例函数 在同一直角坐标系中图象如图,A点为(-2,0)。则下列结论中,正确的是【 】
在同一直角坐标系中图象如图,A点为(-2,0)。则下列结论中,正确的是【 】



