题目内容
如图,某排水管模截面,已知原有积水的水平面宽CD=0.8m时最大水深0.2m,当水面上升0.2m时水面宽多少?
【答案】分析:如图,AB为水面上升0.2m时水面宽,CD=0.8m,过O作OH⊥AB于H,交CD于F,交⊙O于E,则EF=0.2m,FH=0.2m,连OA,OC,则CF=DF=0.4m,AH=BH,设⊙O的半径为R,在Rt△OCF中,OF=R-0.2,利用勾股定理可求出R=0.5;在Rt△OAH中,利用勾股定理得到AH,即可得到水面上升0.2m时水面宽AB.
解答: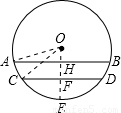 解:如图,
解:如图,
AB为水面上升0.2m时水面宽,CD=0.8m,
过O作OH⊥AB于H,交CD于F,交⊙O于E,则EF=0.2m,FH=0.2m,连OA,OC,
∵OH⊥AB,
∴OF⊥CD,
∴CF=DF=0.4m,AH=BH,
设⊙O的半径为R,
在Rt△OCF中,OF=R-0.2,
∴R2=(R-0.2)2+0.42,
解得R=0.5,
在Rt△OAH中,OH=R-0.4=0.1,
∴AH=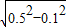 =
=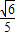 ,
,
∴AB=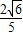 m.
m.
即当水面上升0.2m时水面宽为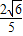 m.
m.
点评:本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了勾股定理.
解答:
 解:如图,
解:如图,AB为水面上升0.2m时水面宽,CD=0.8m,
过O作OH⊥AB于H,交CD于F,交⊙O于E,则EF=0.2m,FH=0.2m,连OA,OC,
∵OH⊥AB,
∴OF⊥CD,
∴CF=DF=0.4m,AH=BH,
设⊙O的半径为R,
在Rt△OCF中,OF=R-0.2,
∴R2=(R-0.2)2+0.42,
解得R=0.5,
在Rt△OAH中,OH=R-0.4=0.1,
∴AH=
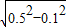 =
=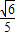 ,
,∴AB=
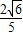 m.
m.即当水面上升0.2m时水面宽为
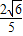 m.
m.点评:本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了勾股定理.

练习册系列答案
相关题目
 如图,某排水管模截面,已知原有积水的水平面宽CD=0.8m时最大水深0.2m,当水面上升0.2m时水面宽多少?
如图,某排水管模截面,已知原有积水的水平面宽CD=0.8m时最大水深0.2m,当水面上升0.2m时水面宽多少? 如图,某排水管模截面,已知原有积水的水平面宽CD=0.8m时最大水深0.2m,当水面上升0.2m时水面宽多少?
如图,某排水管模截面,已知原有积水的水平面宽CD=0.8m时最大水深0.2m,当水面上升0.2m时水面宽多少?
