Question

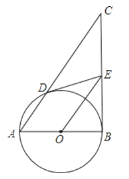
【题目】如图，为测量江两岸码头B、D之间的距离，从山坡上高度为50米的A处测得码头B的俯角∠EAB为15°，码头D的俯角∠EAD为45°，点C在线段BD的延长线上，AC⊥BC，垂足为C，求码头B、D的距离（结果保留整数）．

Answer 1

【答案】135米

【解析】解：∵AE∥BC，∴∠ADC=∠EAD=45°。

又∵AC⊥CD，∴CD=AC=50。

∵AE∥BC，∴∠ABC=∠EAB=15°。

又∵， ∴。

∴BD≈185.2﹣50≈135（米）。

答：码头B、D的距离约为135米。

由∠EAB=15°，根据平行的性质，可得∠ABC=∠EAB=15°。从而解直角三角形ABC可求得BC的长。由∠ADC=∠EAD=45°可得CD=AC=50。从而由BD=BC－CD可求得B、D的距离。