题目内容
王师傅在楼顶上的点A出测得楼前一棵树CD的顶端C的俯角为60°,又知水平距离BD=10cm,楼高AB=24cm,则树高CD为( )
A、(24-10
| ||||
B、(24-
| ||||
C、(24-5
| ||||
| D、9m |
分析:根据题意画出图形,作出辅助线,再利用直角三角形的性质解答即可.
解答: 解:如图所示,
解:如图所示,
AB=24m,BD=10m,∠CAF=60°,
作CE⊥AB于点E,则CE=BD=10m,
∵∠CAF=60°,
∴∠CAE=30°,
在Rt△ACE中,
AE=
=
=10
,
∴CD=BE=(24-10
)m.
故选A.
 解:如图所示,
解:如图所示,AB=24m,BD=10m,∠CAF=60°,
作CE⊥AB于点E,则CE=BD=10m,
∵∠CAF=60°,
∴∠CAE=30°,
在Rt△ACE中,
AE=
| CE |
| tan∠CAE |
| 10 | ||||
|
| 3 |
∴CD=BE=(24-10
| 3 |
故选A.
点评:本题考查的是解直角三角形的应用-仰角俯角问题,根据题意画出图形作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
王师傅在楼顶上的点A处测得楼前一棵树CD的顶端C的俯角为60°,又知水平距离BD=10m,楼高AB=24m,则树高CD为( )
A、(24-10
| ||||
B、(24-
| ||||
C、(24-5
| ||||
| D、9m |
王师傅在楼顶上的点A出测得楼前一棵树CD的顶端C的俯角为60。。,又知水平距离BD=10cm,楼高AB=24cm,则树高CD为( )。
A.(24-10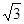 )m )m | B.(24-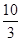 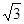 m m | C.(24-5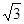 )m )m | D.9m |
 )m B、(24-
)m B、(24-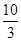
 )m
)m )m
)m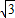 )m
)m