Question

如图，是某个公园ABCDEF，M为AB的中点，N为CD的中点，P为DE的中点，Q为FA的中点，其中游览区APEQ与BNDM的面积和是900平方米，中间的湖水面积为361平方米，其余的部分是草地，则草地的总面积是________平方米．

Answer 1

539
分析：连接AD、AE、DB，根据一个三角形的中线平分这个三角形的面积，可知：△EQA面积=△EQF面积，△AEP面积=△ADP面积，△DBM面积=△DAM面积，△BND面积=△BNC面积上述四个等式相加，即可求解．
解答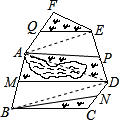：解：连接AE、AD，BD．
因为M为AB的中点，N为CD的中点，P为DE的中点，Q为FA的中点，
根据一个三角形的中线平分这个三角形的面积，
所以设S_△EFQ=S_△AQE=a，
S_△AEP=S_△APD=b，
S_△ADM=S_△BDM=c，
S_△BDN=S_△BCN=d．
因为游览区APEQ与BNDM的面积和是900平方米，中间湖水AMDP的面积是361平方米，
即a+b+c+d=900平方米，b+c=361平方米
所以a+d=900-361=539平方米
即草地的总面积S_△EFQ+S_△BCN=a+d=539平方米．
故答案为：539．
点评：此题主要考查了三角形的面积公式，用规则的图形表示出不规则的图形是解题的关键．